题目内容
长方形ABCD中,AD=10,AB=8,将长方形ABCD折叠,折痕为EF
(1)当A′与B重合时(如图1),EF= ;
(2)当直线EF过点D时(如图2),点A的对应点A′落在线段BC上,求线段EF的长;
(3)如图3,点A的对应点A′落在线段BC上,E点在线段AB上,同时F点也在线段AD上,则A′B的距离是 ;
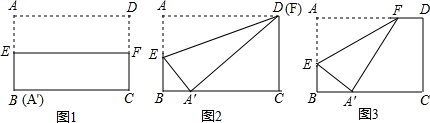
(1)当A′与B重合时(如图1),EF=
(2)当直线EF过点D时(如图2),点A的对应点A′落在线段BC上,求线段EF的长;
(3)如图3,点A的对应点A′落在线段BC上,E点在线段AB上,同时F点也在线段AD上,则A′B的距离是

考点:翻折变换(折叠问题)
专题:
分析:(1)根据题意结合图形直接写出答案即可解决问题;
(2)根据勾股定理首先求出A′C的长度;再次利用勾股定理求出AE的长度,即可解决问题.
(3)如图(3),作辅助线,证明△EBA′∽△A′GF,列出比例式得到关于有关线段的方程,解方程即可解决问题.
(2)根据勾股定理首先求出A′C的长度;再次利用勾股定理求出AE的长度,即可解决问题.
(3)如图(3),作辅助线,证明△EBA′∽△A′GF,列出比例式得到关于有关线段的方程,解方程即可解决问题.
解答: 解:(1)如图1,当A′与B重合时,EF=10;
解:(1)如图1,当A′与B重合时,EF=10;
(2)如图2,设AE=x,则BE=8-x;
∵四边形ABCD为矩形,
∴BC=AD=10,DC=AB=8;∠B=∠C=90°;
由题意得:A′D=AD=10;
由勾股定理得:
A′C2=A′D2-DC2=100-64=36,
∴A′C=6,BA′=10-6=4;
在直角△A′BE中,由勾股定理得:
x2=(8-x)2+42,
解得:x=5,
由勾股定理得:EF2=102+52=125,
∴EF=5
.
(3)如图3,过点F作FG⊥BC于点G;
设AE=x.,AF=y;
由题意得:
A′E=AE=x,A′F=AF=y,BG=AF=y;
则BE=8-x,A′B=
=
,
∴A′G=y-
;
由题意知:∠B=∠EA′F=∠A′GF=90°,
∴∠BEA′+∠BA′E=∠BA′E+∠FA′G,
∴∠BEA′=∠FA′G,而∠B=∠A′GF,
∴△EBA′∽△A′GF,
∴CE=
;
∴
=
=
,
即
=
=
,
解该方程得:x=5,y=10,
∴A′B=
=
=4,
即A′B的距离是4.
 解:(1)如图1,当A′与B重合时,EF=10;
解:(1)如图1,当A′与B重合时,EF=10;(2)如图2,设AE=x,则BE=8-x;
∵四边形ABCD为矩形,
∴BC=AD=10,DC=AB=8;∠B=∠C=90°;
由题意得:A′D=AD=10;
由勾股定理得:
A′C2=A′D2-DC2=100-64=36,
∴A′C=6,BA′=10-6=4;
在直角△A′BE中,由勾股定理得:
x2=(8-x)2+42,
解得:x=5,
由勾股定理得:EF2=102+52=125,
∴EF=5
| 5 |
(3)如图3,过点F作FG⊥BC于点G;
设AE=x.,AF=y;
由题意得:
A′E=AE=x,A′F=AF=y,BG=AF=y;
则BE=8-x,A′B=
| x2-(8-x)2 |
| 16x-64 |
∴A′G=y-
| 16x-64 |
由题意知:∠B=∠EA′F=∠A′GF=90°,
∴∠BEA′+∠BA′E=∠BA′E+∠FA′G,
∴∠BEA′=∠FA′G,而∠B=∠A′GF,
∴△EBA′∽△A′GF,
∴CE=
| CA•CB |
| CD |
∴
| BE |
| A′G |
| BA′ |
| GF |
| EA′ |
| A′F |
即
| 8-x | ||
y-
|
| ||
| 8 |
| x |
| y |
解该方程得:x=5,y=10,
∴A′B=
| 16×5-64 |
| 16 |
即A′B的距离是4.
点评:该命题主要考查了翻折变换及其应用问题;解题的关键是根据翻折变换的性质准确找出命题图形中隐含的等量关系,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
下列各组数中,都是无理数的一组是( )
A、-
| |||||
B、
| |||||
C、
| |||||
D、
|
在数轴上,点A表示的数为4,点B表示的数为-2,则AB两点之间的距离为( )
| A、-6 | B、2 | C、-2 | D、6 |
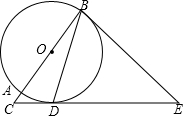 如图,AB为⊙O的直径,C为BA的延长线上一点,D为⊙O上一点,且∠CDA=∠CBD.
如图,AB为⊙O的直径,C为BA的延长线上一点,D为⊙O上一点,且∠CDA=∠CBD.
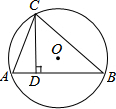 如图,△ABC内接于⊙O,CD是△ABC的高,CD=6,AD=3,BD=8,求⊙O的面积.
如图,△ABC内接于⊙O,CD是△ABC的高,CD=6,AD=3,BD=8,求⊙O的面积.