题目内容
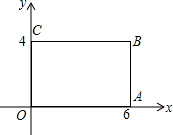 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的| 1 |
| 4 |
考点:位似变换,坐标与图形性质
专题:
分析:利用位似图形的性质得出位似比,进而得出对应点的坐标.
解答:解:∵矩形OA′B′C′的面积等于矩形OABC面积的
,
∴两矩形面积的相似比为:1:2,
∵B的坐标是(6,4),∴点B′的坐标是:(3,2)或(-3,-2).
故答案为:(3,2)或(-3,-2).
| 1 |
| 4 |
∴两矩形面积的相似比为:1:2,
∵B的坐标是(6,4),∴点B′的坐标是:(3,2)或(-3,-2).
故答案为:(3,2)或(-3,-2).
点评:此题主要考查了位似变换的性质,得出位似图形对应点坐标性质是解题关键.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
在数轴上,点A表示的数为4,点B表示的数为-2,则AB两点之间的距离为( )
| A、-6 | B、2 | C、-2 | D、6 |
如图所示图形中,不是正方体的展开图的是( )
A、 |
B、 |
C、 |
D、 |
⊙O的半径为8,点A在直线l上,若OA=8,则直线l与⊙O的位置关系是( )
| A、相离 | B、相切 |
| C、相交 | D、相切或相交 |
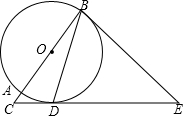 如图,AB为⊙O的直径,C为BA的延长线上一点,D为⊙O上一点,且∠CDA=∠CBD.
如图,AB为⊙O的直径,C为BA的延长线上一点,D为⊙O上一点,且∠CDA=∠CBD.