题目内容
边长为a的正三角形的边心距、半径(外接圆的半径)和高之比为 .
考点:正多边形和圆
专题:
分析:连接OB,AO,延长AO交BC于D,根据⊙O是等边三角形ABC的外接圆求出∠OBC=30°,推出OB=2OD,求出AD=
OB,代入求出即可.
| 3 |
| 2 |
解答: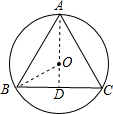 解:连接OB,AO,延长AO交BC于D,
解:连接OB,AO,延长AO交BC于D,
∵⊙O是等边三角形ABC的外接圆,
∴AD⊥BC,∠OBC=
∠ABC=
×60°=30°,
∴BD=
a.
∵∠ADB=90°,∠OBC=30°,
∴OD=
,OB=
a,AD=AB•cos30°=
,
∴边长为a的正三角形的边心距、半径(外接圆的半径)和高之比=OD:OB:AD=
:
a:
=1:2:3.
故答案为:1:2:3.
 解:连接OB,AO,延长AO交BC于D,
解:连接OB,AO,延长AO交BC于D,∵⊙O是等边三角形ABC的外接圆,
∴AD⊥BC,∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴BD=
| 1 |
| 2 |
∵∠ADB=90°,∠OBC=30°,
∴OD=
| ||
| 12 |
| ||
| 6 |
| ||
| 2 |
∴边长为a的正三角形的边心距、半径(外接圆的半径)和高之比=OD:OB:AD=
| ||
| 12 |
| ||
| 6 |
| ||
| 2 |
故答案为:1:2:3.
点评:本题考查的是正多边形和圆,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
下列计算正确的是( )
| A、(2x+3y)2=4x2+9y2 | ||||||||||
B、(-c+
| ||||||||||
C、(
| ||||||||||
| D、(2a+5b)2=4a2+10ab+25b2 |
小明家距学校m千米,一天他从家上学先以a千米/时的匀速跑步锻炼前进,后以匀速b千米/时步行到达学校,共用n小时.下图中能够反映小明同学距学校的距离s(千米)与上学的时间t(小时)之间的大致图象是( )
A、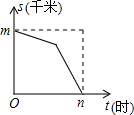 |
B、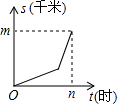 |
C、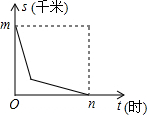 |
D、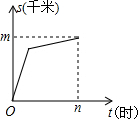 |
 如图所示,关于线段、射线和直线的条数,下列说法正确的是( )
如图所示,关于线段、射线和直线的条数,下列说法正确的是( )| A、五条线段,三条射线 |
| B、一条直线,三条线段 |
| C、三条线段,两条射线,一条直线 |
| D、三条线段,三条射线 |
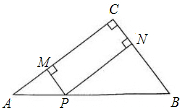 如图,在△ABC中,∠C=90°,AC=8,BC=6,P是AB边上的一个动点(异于A、B两点),过点P分别作AC、BC边的垂线,垂足分别为M、N,设AP=x.
如图,在△ABC中,∠C=90°,AC=8,BC=6,P是AB边上的一个动点(异于A、B两点),过点P分别作AC、BC边的垂线,垂足分别为M、N,设AP=x.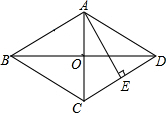 在菱形ABCD中,对角线AC与BD相交于点O,AE⊥CD于点E,且AE=OD,求∠ADC的度数.
在菱形ABCD中,对角线AC与BD相交于点O,AE⊥CD于点E,且AE=OD,求∠ADC的度数.