题目内容
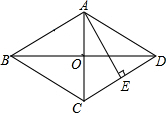 在菱形ABCD中,对角线AC与BD相交于点O,AE⊥CD于点E,且AE=OD,求∠ADC的度数.
在菱形ABCD中,对角线AC与BD相交于点O,AE⊥CD于点E,且AE=OD,求∠ADC的度数.考点:菱形的性质
专题:
分析:根据菱形的性质得出AD=DC,AC⊥BD,根据HL证Rt△AOD≌Rt△DEA,求出∠DAO=∠ADE,求出△ADC是等边三角形即可.
解答:解:∵四边形ABCD是菱形,
∴AD=DC,AC⊥BD,
∵AE⊥CD,
∴∠DOA=∠AED=90°,
在Rt△AOD和Rt△DEA中
∴Rt△AOD≌Rt△DEA(HL),
∴∠DAO=∠ADE,
∵AD=DC,
∴∠DAC=∠DCA,
∴∠DAC=∠DCA=∠ADC,
∴△ADC是等边三角形,
∴∠ADC=60°.
∴AD=DC,AC⊥BD,
∵AE⊥CD,
∴∠DOA=∠AED=90°,
在Rt△AOD和Rt△DEA中
|
∴Rt△AOD≌Rt△DEA(HL),
∴∠DAO=∠ADE,
∵AD=DC,
∴∠DAC=∠DCA,
∴∠DAC=∠DCA=∠ADC,
∴△ADC是等边三角形,
∴∠ADC=60°.
点评:本题考查了全等三角形的性质和判定,等边三角形的性质和判定,菱形的性质的应用,能综合运用性质进行推理是解此题的关键,注意:菱形的四条边都相等,菱形的对角线互相垂直.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
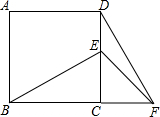 在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针旋转90°,得到△DFC,连接EF,若∠BEC=60°,则∠EFD等于( )
在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针旋转90°,得到△DFC,连接EF,若∠BEC=60°,则∠EFD等于( )| A、10° | B、25° |
| C、20° | D、15° |

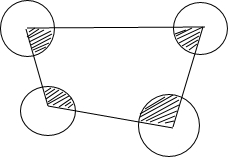 如图所示,分别以四边形的各个顶点为圆心,半径为10作圆(这些圆互不相交).问这些圆与四边形的公共部分(即图中阴影部分)的面积是多少?为什么?
如图所示,分别以四边形的各个顶点为圆心,半径为10作圆(这些圆互不相交).问这些圆与四边形的公共部分(即图中阴影部分)的面积是多少?为什么?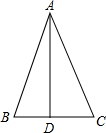 如图,在△ABC中,AB=AC,AD是BC边上的高,∠C=63°,BC=4,求∠BAD的度数及DC的长.
如图,在△ABC中,AB=AC,AD是BC边上的高,∠C=63°,BC=4,求∠BAD的度数及DC的长. 如图,直线y=-
如图,直线y=-