题目内容
8.(1)解方程:x2-6x+8=0;(2)解不等式组:$\left\{\begin{array}{l}{2(x-1)≥x+1}\\{x-2>\frac{1}{3}(2x-1)}\end{array}\right.$.
分析 (1)先把方程左边分解,使原方程转化为x-2=0或x-6=0,然后解两个一次方程即可.
(2)先求出两个不等式的解集,再求其公共解.
解答 解:(1)由原方程,得
(x-2)(x-4)=0,
x-2=0或x-4=0,
所以x1=2,x2=4.
(2)由原不等式得到:$\left\{\begin{array}{l}{x-3≥0①}\\{x-5>0②}\end{array}\right.$,
解不等式①得:x≥3.
解不等式②得:x>5.
故原不等式组的解集是x>5.
点评 本题考查了解一元二次方程--因式分解法,解一元一次不等式组.解不等式时,观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
3.下列命题错误的是( )
| A. | 平行四边形的对角相等 | B. | 正方形的对角线相等 | ||
| C. | 对角线相等的平行四边形是矩形 | D. | 对角线互相垂直的四边形是菱形 |
13.设$\sqrt{2}=a,\sqrt{3}=b$,用含a、b的式子表示$\sqrt{0.54}$,下列表示正确的是( )
| A. | $\frac{3ab}{10}$ | B. | 3ab | C. | $\frac{{{a^2}{b^2}}}{10}$ | D. | $\frac{{{a^3}b}}{10}$ |
18.若分式$\frac{x+y}{2xy}$中的x、y的值都变为原来的3倍,则此分式的值( )
| A. | 不变 | B. | 是原来的3倍 | C. | 是原来的$\frac{1}{3}$ | D. | 不能确定 |
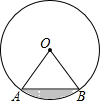 如图,已知圆O的半径是2,∠AOB=60°,则阴影部分的面积为$\frac{2}{3}$π-$\sqrt{3}$(结果可π表示)
如图,已知圆O的半径是2,∠AOB=60°,则阴影部分的面积为$\frac{2}{3}$π-$\sqrt{3}$(结果可π表示)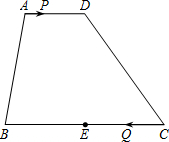 如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒8个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间t=$\frac{2}{7}$或$\frac{14}{9}$秒时,以点P、Q、E、D为顶点的四边形是平行四边形.
如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒8个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间t=$\frac{2}{7}$或$\frac{14}{9}$秒时,以点P、Q、E、D为顶点的四边形是平行四边形.