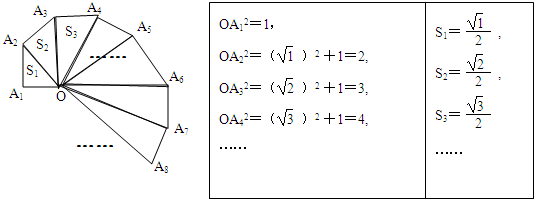题目内容
9.等腰△ABC中,过A作BC的垂线,垂足为D,且AD=$\frac{1}{2}$BC,则△ABC底角的度数为( )| A. | 45° | B. | 45°或75° | C. | 45°或15°或75° | D. | 45°或60° |
分析 分三种情况讨论,先根据题意分别画出图形,当AB=AC时,根据已知条件得出AD=BD=CD,从而得出△ABC底角的度数;当AB=BC时,先求出∠ABD的度数,再根据AB=BC,求出底角的度数;当AB=BC时,根据AD=$\frac{1}{2}$BC,AB=BC,得出∠DBA=30°,从而得出底角的度数.
解答  解:①如图1,当AB=AC时,
解:①如图1,当AB=AC时,
∵AD⊥BC,
∴BD=CD,
∵AD=$\frac{1}{2}$BC,
∴AD=BD=CD,
∴底角为45°;
②如图2,当AB=BC时,
∵AD=$\frac{1}{2}$BC,
∴AD=$\frac{1}{2}$AB,
∴∠ABD=30°,
∴∠BAC=∠BCA=75°,
∴底角为75°.
③如图3,当AB=BC时,
∵AD=$\frac{1}{2}$BC,AB=BC,
∴AD=$\frac{1}{2}$AB,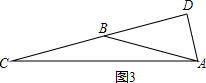
∴∠DBA=30°,
∴∠BAC=∠BCA=15°;
∴△ABC底角的度数为45°或75°或15°.
故选C.
点评 本题考查了30°角所对的直角边等于斜边的一半的性质,等腰三角形的两底角相等的性质,以及三角形的一个外角等于与它不相邻的两个内角的和的性质,难点在于要分情况讨论求解.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
20.正方形ABCD中,E,F分别为AB,BC的中点,AF与DE相交于点O,则$\frac{DO}{AD}$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$$\sqrt{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
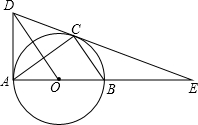 如图,AB是⊙O的直径,点C在⊙O上,连接BC、AC,作OD∥BC,与过点A的切线交于点D,连接DC并延长交AB的延长线于点E
如图,AB是⊙O的直径,点C在⊙O上,连接BC、AC,作OD∥BC,与过点A的切线交于点D,连接DC并延长交AB的延长线于点E