题目内容
8.【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a-b|,线段AB的中点表示的数为$\frac{a+b}{2}$.【问题情境】如图,数轴上点A表示的数为-2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.
设运动时间为t秒(t>0).
【综合运用】
(1)填空:
①A、B两点间的距离AB=10,线段AB的中点表示的数为3;
②用含t的代数式表示:t秒后,点P表示的数为-2+3t;点Q表示的数为8-2t.
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=$\frac{1}{2}$AB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.

分析 (1)根据题意即可得到结论;
(2)当P、Q两点相遇时,P、Q表示的数相等列方程得到t=2,于是得到当t=2时,P、Q相遇,即可得到结论;
(3)由t秒后,点P表示的数-2+3t,点Q表示的数为8-2t,于是得到PQ=|(-2+3t)-(8-2t)|=|5t-10|,列方程即可得到结论;
(4)由点M表示的数为 $\frac{-2+(-2+3t)}{2}$=$\frac{3t}{2}$-2,点N表示的数为 $\frac{8+(-2+3t)}{2}$=$\frac{3t}{2}$+3,即可得到结论.
解答 解:(1)①10,3;
②-2+3t,8-2t;
(2)∵当P、Q两点相遇时,P、Q表示的数相等
∴-2+3t=8-2t,
解得:t=2,
∴当t=2时,P、Q相遇,
此时,-2+3t=-2+3×2=4,
∴相遇点表示的数为4;
(3)∵t秒后,点P表示的数-2+3t,点Q表示的数为8-2t,
∴PQ=|(-2+3t)-(8-2t)|=|5t-10|,
又PQ=$\frac{1}{2}$AB=$\frac{1}{2}$×10=5,
∴|5t-10|=5,
解得:t=1或3,
∴当:t=1或3时,PQ=$\frac{1}{2}$AB;
(4)∵点M表示的数为 $\frac{-2+(-2+3t)}{2}$=$\frac{3t}{2}$-2,
点N表示的数为 $\frac{8+(-2+3t)}{2}$=$\frac{3t}{2}$+3,
∴MN=|($\frac{3t}{2}$-2)-($\frac{3t}{2}$+3)|=|$\frac{3t}{2}$-2-$\frac{3t}{2}$-3|=5.
点评 本题考查了一元一次方程的应用应用和数轴,解题的关键是掌握点的移动与点所表示的数之间的关系,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

| A. | ①②均用代入法 | B. | ①②均用加减法 | ||
| C. | ①用代入法,②用加减法 | D. | ①用加减法,②用代入法 |
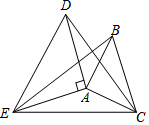 如图,△ABC和△ADE都是等腰直角三角形,∠EAD=∠BAC=90°,∠DAB=45°,连接BE,DC,EC,则下列说法正确的有( )
如图,△ABC和△ADE都是等腰直角三角形,∠EAD=∠BAC=90°,∠DAB=45°,连接BE,DC,EC,则下列说法正确的有( )①BE=DC②AD∥BC③BE=DE④BE=EC.
| A. | ①③ | B. | ②④ | C. | ①②④ | D. | ①②③④ |
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
 如图,在网格图中,每个小正方形的顶点叫做格点,以格点为顶点的三角形叫做格点三角形,且每个小正方形的边长均为1,三角形ABC为一格点三角形,认真观察图形,请你求出三角形ABC的面积.
如图,在网格图中,每个小正方形的顶点叫做格点,以格点为顶点的三角形叫做格点三角形,且每个小正方形的边长均为1,三角形ABC为一格点三角形,认真观察图形,请你求出三角形ABC的面积.