题目内容
9.如果从-1,2,3三个数中任取一个数记作m,又从0,1,-2三个数中任取一个数记作n,那么点P(m,n)恰在第四象限的概率为( )| A. | $\frac{2}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
分析 画树状图展示所有9种等可能的结果数,再根据第四象限内点的坐标特征找出点P(m,n)恰在第四象限的结果数,然后根据概率公式求解.
解答 解:画树状图为:
共有9种等可能的结果数,其中点P(m,n)恰在第四象限的结果数为2,
所以点P(m,n)恰在第四象限的概率=$\frac{2}{9}$.
故选A.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
17.我们规定一个物体向右运动为正,向左运动为负.如果该物体向左连续运动两次,每次运动3 米,那么下列算式中,可以表示这两次运动结果的是( )
| A. | (-3)2 | B. | (-3)-(-3) | C. | 2×3 | D. | 2×(-3) |
4.若二次函数y=x2-2x+c的图象与x轴没有交点,则c的值可能是( )
| A. | -3 | B. | -2 | C. | 0 | D. | 2 |
14.已知△ABC的三边长分别为1、k、3,则化简|9-2k|-$\sqrt{4{k}^{2}-12k+9}$的结果是( )
| A. | 12-4k | B. | 6 | C. | -6 | D. | 4k-12 |
1.二次函数y=ax2+bx+c中,y与x的部分对应值如下表:
根据表格,小明得出三个结论:①ac<0;②当x=2时,y=5;③x=3是方程ax2+(b-1)x+c=0的一个根,其中结论正确的共有( )
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
| A. | 0 个 | B. | 1个 | C. | 2个 | D. | 3个 |
18.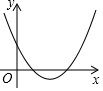 二次函数y=2x2-2x+m(m为常数)的图象如图所示,如果当x=a时,y<0,那么当x=a-1时,函数值( )
二次函数y=2x2-2x+m(m为常数)的图象如图所示,如果当x=a时,y<0,那么当x=a-1时,函数值( )
 二次函数y=2x2-2x+m(m为常数)的图象如图所示,如果当x=a时,y<0,那么当x=a-1时,函数值( )
二次函数y=2x2-2x+m(m为常数)的图象如图所示,如果当x=a时,y<0,那么当x=a-1时,函数值( )| A. | y<0 | B. | 0<y<m | C. | m<y<m+4 | D. | y>m |