题目内容
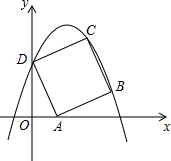 如图,在平面直角坐标系xOy中,边长为
如图,在平面直角坐标系xOy中,边长为| 5 |
(1)写出点B的坐标(
(2)若抛物线y=-
| 5 |
| 6 |
①求b的值;
②根据函数的图象,求出当y>0时x的取值范围.
考点:抛物线与x轴的交点,待定系数法求二次函数解析式,正方形的性质
专题:
分析:(1)过C点和B点分别作x轴和y轴的垂线,根据和△AOD的关系,写出各点的坐标.
(2)①根据点B的坐标来求b的值;
②利用①中的函数关系式求得抛物线与x轴的交点坐标,然后结合图象进行答题.
(2)①根据点B的坐标来求b的值;
②利用①中的函数关系式求得抛物线与x轴的交点坐标,然后结合图象进行答题.
解答: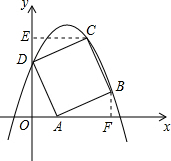 解:(1)∵点A的坐标(1,0),
解:(1)∵点A的坐标(1,0),
∴OA=1.
又∵AD=
,
∴由勾股定理知,OD=
=
=2,即OD=2.
如图,过点C作CE⊥y轴于E,过点B作bF⊥y于F,
在△AOD与△BFA中,
,
∴△AOD≌△BFA(AAS),
∴AO=BF=1,OD=FA=2,
∴OF=OA+OD=3,
∴B(3,1).
同理,△CED≌△DOA,则CE=DO=2,ED=OA=1,
∴OE=OD+ED=3,
∴C(2,3).
故答案是:3;1;2;3;
(2)①由(1)知,B(3,1).
把B(3,1)代入y=-
x2+bx+2,得
1=-
×32+3b+2,
解得 b=
;
②由①得到抛物线的解析式为:y=-
x2+
x+2.
令y=0,则-
x2+
x+2=0,
整理,得
5x2-13x-12=0.
解得 x=
.
所以,该抛物线与x轴两个交点的横坐标分别是
、
.
所以,根据图象知,当y>0时x的取值范围是
<x<
.
 解:(1)∵点A的坐标(1,0),
解:(1)∵点A的坐标(1,0),∴OA=1.
又∵AD=
| 5 |
∴由勾股定理知,OD=
| AD2-OA2 |
| 5-1 |
如图,过点C作CE⊥y轴于E,过点B作bF⊥y于F,
在△AOD与△BFA中,
|
∴△AOD≌△BFA(AAS),
∴AO=BF=1,OD=FA=2,
∴OF=OA+OD=3,
∴B(3,1).
同理,△CED≌△DOA,则CE=DO=2,ED=OA=1,
∴OE=OD+ED=3,
∴C(2,3).
故答案是:3;1;2;3;
(2)①由(1)知,B(3,1).
把B(3,1)代入y=-
| 5 |
| 6 |
1=-
| 5 |
| 6 |
解得 b=
| 13 |
| 6 |
②由①得到抛物线的解析式为:y=-
| 5 |
| 6 |
| 13 |
| 6 |
令y=0,则-
| 5 |
| 6 |
| 13 |
| 6 |
整理,得
5x2-13x-12=0.
解得 x=
13±
| ||
| 10 |
所以,该抛物线与x轴两个交点的横坐标分别是
13-
| ||
| 10 |
13+
| ||
| 10 |
所以,根据图象知,当y>0时x的取值范围是
13-
| ||
| 10 |
13+
| ||
| 10 |
点评:本题考查了待定系数法求解析式以及正方形的性质,坐标与图形的性质的知识点.

练习册系列答案
相关题目
 已知三角形的中线,通常把中线延长一倍,构造全等三角形.如图,△ABC中,AD是中线,AD也是角平分线,求证:△ABC是等腰三角形.
已知三角形的中线,通常把中线延长一倍,构造全等三角形.如图,△ABC中,AD是中线,AD也是角平分线,求证:△ABC是等腰三角形.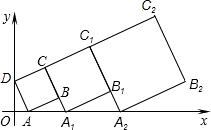 在平面直角坐标系xOy中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第1个正方形的面积为
在平面直角坐标系xOy中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第1个正方形的面积为 如图,在△ABC中,已知∠BAC=90°,AD⊥BC于D,E是AB上一点,AF⊥CE于F,AD交CE于G点,
如图,在△ABC中,已知∠BAC=90°,AD⊥BC于D,E是AB上一点,AF⊥CE于F,AD交CE于G点,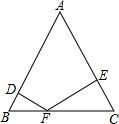 如图,△ABC为等边三角形,边长为4,F为BC边上一个动点(不与B,C重合),DF⊥AB,EF⊥AC,垂足分别为D和E.
如图,△ABC为等边三角形,边长为4,F为BC边上一个动点(不与B,C重合),DF⊥AB,EF⊥AC,垂足分别为D和E.
 已知:BE⊥CD,BE=DE,BC=DA,∠B=∠D.求证:
已知:BE⊥CD,BE=DE,BC=DA,∠B=∠D.求证: