题目内容
18.在平面直角坐标系xOy中,一次函数y=8-x的图象与函数y=$\frac{8}{x}$(x>0)的图象相交于点A,B,设点A的坐标为(x1,y1),那么长为x1,宽为y1的矩形的面积为8,周长为16.分析 根据已知得出x1y1=8,x1+y1=8,求出A的坐标,再根据矩形的性质求出面积和周长即可.
解答 解:∵点A在函数y=$\frac{8}{x}$(x>0)的图象上,
∴x1y1=8,
又∵点A在函数y=8-x上,
∴x1+y1=8,
∴矩形的周长为2(x1+y1)=16,
故答案为:8,16.
点评 此题主要考查了一次函数与反比例函数的交点问题,根据函数关系式中系数的意义直接求解,没必要求出交点坐标,难易程度适中.

练习册系列答案
相关题目
7.点P1(2,y1),P2(4,y2)是一次函数y=(m-2)x+m图象上的两个点,若y1<y2,则m的取值范围是( )
| A. | m>0 | B. | m<0 | C. | m>2 | D. | m<2 |
8.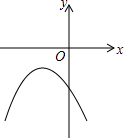 二次函数y=ax2+bx+c的图象如图所示,则下列判断正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列判断正确的是( )
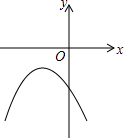 二次函数y=ax2+bx+c的图象如图所示,则下列判断正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列判断正确的是( )| A. | a>0 | B. | b>0 | C. | c>0 | D. | abc<0 |
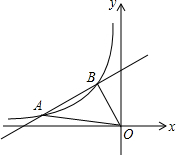 如图,已知一次函数y=$\frac{1}{2}$x+b与反比例函数y=$\frac{m}{x}$在第二象限的图象交于A(n,$\frac{1}{2}$)、B(-1,2)两点.
如图,已知一次函数y=$\frac{1}{2}$x+b与反比例函数y=$\frac{m}{x}$在第二象限的图象交于A(n,$\frac{1}{2}$)、B(-1,2)两点.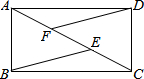 如图所示,E,F是矩形ABCD对角线AC上的两点,试添加一个条件:AF=CE,使得BE∥DF.
如图所示,E,F是矩形ABCD对角线AC上的两点,试添加一个条件:AF=CE,使得BE∥DF.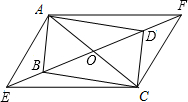 如图,?ABCD的对角线相交于点O,E、F在直线BD上,且BE=DF.
如图,?ABCD的对角线相交于点O,E、F在直线BD上,且BE=DF.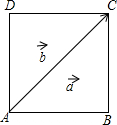 如图,在正方形ABCD中,如果AC=3$\sqrt{2}$,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么|$\overrightarrow{a}$-$\overrightarrow{b}$|=3.
如图,在正方形ABCD中,如果AC=3$\sqrt{2}$,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么|$\overrightarrow{a}$-$\overrightarrow{b}$|=3. 已知:如图,△ABC中,∠BAC=90°,点D在BC边上,且BD=BA,过点B画AD的垂线交AC于点O,以O为圆心,AO为半径画圆.
已知:如图,△ABC中,∠BAC=90°,点D在BC边上,且BD=BA,过点B画AD的垂线交AC于点O,以O为圆心,AO为半径画圆.