题目内容
3.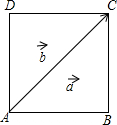 如图,在正方形ABCD中,如果AC=3$\sqrt{2}$,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么|$\overrightarrow{a}$-$\overrightarrow{b}$|=3.
如图,在正方形ABCD中,如果AC=3$\sqrt{2}$,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么|$\overrightarrow{a}$-$\overrightarrow{b}$|=3.
分析 首先由在正方形ABCD中,如果AC=3$\sqrt{2}$,可求得BC的长,又由$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,可得|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{BC}$|=BC.
解答 解:∵在正方形ABCD中,AC=3$\sqrt{2}$,
∴AB=BC=3,
∵$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,
∴$\overrightarrow{a}$-$\overrightarrow{b}$=$\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$,
∴|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{BC}$|=BC=3.
故答案为:3.
点评 此题考查了平面向量的知识.注意掌握三角形法则的应用.

练习册系列答案
相关题目
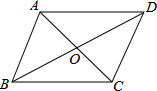 如图,平行四边形ABCD的对角线相交于点O,请你添加一个条件AC=BD.答案不唯一..(只添一个即可),使平行四边形ABCD是矩形.
如图,平行四边形ABCD的对角线相交于点O,请你添加一个条件AC=BD.答案不唯一..(只添一个即可),使平行四边形ABCD是矩形. 如图是由梯子A B和梯子AC搭成的脚手架,其中AB=AC=5米,∠α=70°.
如图是由梯子A B和梯子AC搭成的脚手架,其中AB=AC=5米,∠α=70°.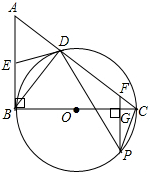 如图,已知,在△ABC中,∠ABC=90°,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
如图,已知,在△ABC中,∠ABC=90°,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F. 看图回答问题:
看图回答问题: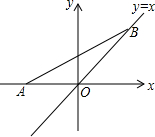 如图,点A的坐标为(-$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB最短时,求点B的坐标.
如图,点A的坐标为(-$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB最短时,求点B的坐标.