题目内容
8.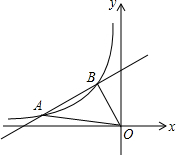 如图,已知一次函数y=$\frac{1}{2}$x+b与反比例函数y=$\frac{m}{x}$在第二象限的图象交于A(n,$\frac{1}{2}$)、B(-1,2)两点.
如图,已知一次函数y=$\frac{1}{2}$x+b与反比例函数y=$\frac{m}{x}$在第二象限的图象交于A(n,$\frac{1}{2}$)、B(-1,2)两点.(1)求m、n的值;
(2)根据图象回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(3)△AOB的面积是多少?
分析 (1)利用反比例函数图象上点的坐标特征,将点B(-1,2)代入反比例函数解析式求得m的值;然后将点A的坐标代入反比例函数解析式,列出关于n的方程,解方程求出n的值;
(2)在第二象限内,一次函数的图象在反比例函数图象上方的部分对应的x的取值范围即为所求;
(3)过A、B分别作AF⊥y轴于F,BE⊥y轴于E,根据图形计算S△AOB=S梯形ABEF+S△AOF-S△BOE=S梯形ABEF即可.
解答 解:(1)∵反比例函数y=$\frac{m}{x}$的图象经过点B(-1,2),
∴m=-1×2=-2;
又∵反比例函数y=-$\frac{2}{x}$的图象经过点A(n,$\frac{1}{2}$),
∴n=-2÷$\frac{1}{2}$=-4;
(2)∵一次函数y=$\frac{1}{2}$x+b与反比例函数y=$\frac{m}{x}$在第二象限的图象交于A(-4,$\frac{1}{2}$)、B(-1,2)两点,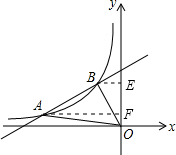 ∴当-4<x<-1时,一次函数大于反比例函数的值;
∴当-4<x<-1时,一次函数大于反比例函数的值;
(3)过A、B分别作AF⊥y轴于F,BE⊥y轴于E,
S△AOB=S梯形ABEF+S△AOF-S△BOE
=S梯形ABEF
=$\frac{1}{2}$×(1+4)×(2-$\frac{1}{2}$)
=$\frac{15}{4}$.
点评 本题考查了反比例函数与一次函数的交点问题,解题时,利用了反比例函数图象上点的坐标特征、待定系数法求反比例函数的解析式.同时要注意运用数形结合的思想.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
18.在平面直角坐标系中,点P(-5,4)位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.已知关于x的方程(x-a)(x-b)-1=0(a<b)的两根为p、q(p<q,且pq>0),则一定有( )
| A. | a<p<q<b | B. | $\frac{q}{p}$>$\frac{b}{a}$ | C. | $\frac{1}{q}$<$\frac{1}{b}$<$\frac{1}{a}$<$\frac{1}{p}$ | D. | $\frac{1}{a}$<$\frac{1}{p}$<$\frac{1}{q}$<$\frac{1}{b}$ |
3.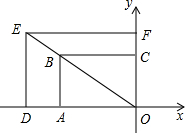 如图,矩形OABC与矩形ODEF是位似图形,点O为位似中心,相似比为1:1.2,点B的坐标为(-3,2),则点E的坐标是( )
如图,矩形OABC与矩形ODEF是位似图形,点O为位似中心,相似比为1:1.2,点B的坐标为(-3,2),则点E的坐标是( )
 如图,矩形OABC与矩形ODEF是位似图形,点O为位似中心,相似比为1:1.2,点B的坐标为(-3,2),则点E的坐标是( )
如图,矩形OABC与矩形ODEF是位似图形,点O为位似中心,相似比为1:1.2,点B的坐标为(-3,2),则点E的坐标是( )| A. | (3.6,2.4) | B. | (-3,2.4) | C. | (-3.6,2) | D. | (-3.6,2.4) |
20.一组数据是4,x,5,10,11共五个数,其平均数为7,则这组数据的众数是( )
| A. | 4 | B. | 5 | C. | 10 | D. | 11 |
17.已知一次函数y=kx-2,若y随x的增大而减小,则该函数的图象经过哪些象限( )
| A. | 二、三、四 | B. | 一、二、三 | C. | 一、三、四 | D. | 一、二、四 |
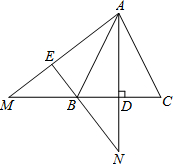 如图,在△ABC中,AB=AC,AD⊥BC于D点,把△ACD绕着A点顺时针旋转,使得AC与AB重合,点D落在点E处,延长AE、CB相交于M点,延长EB、AD相交于N点.求证:AM=AN.
如图,在△ABC中,AB=AC,AD⊥BC于D点,把△ACD绕着A点顺时针旋转,使得AC与AB重合,点D落在点E处,延长AE、CB相交于M点,延长EB、AD相交于N点.求证:AM=AN.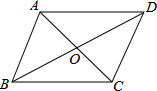 如图,平行四边形ABCD的对角线相交于点O,请你添加一个条件AC=BD.答案不唯一..(只添一个即可),使平行四边形ABCD是矩形.
如图,平行四边形ABCD的对角线相交于点O,请你添加一个条件AC=BD.答案不唯一..(只添一个即可),使平行四边形ABCD是矩形.