题目内容
10. 已知:如图,△ABC中,∠BAC=90°,点D在BC边上,且BD=BA,过点B画AD的垂线交AC于点O,以O为圆心,AO为半径画圆.
已知:如图,△ABC中,∠BAC=90°,点D在BC边上,且BD=BA,过点B画AD的垂线交AC于点O,以O为圆心,AO为半径画圆.(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为8,tan∠C=$\frac{4}{3}$,求线段AB的长,sin∠ADB的值.
分析 (1)连接OD,通过证得△ABO≌△DBO,证得∠ODB=∠OAB=90°,从而证得BD⊥OD,得出BC是⊙O的切线;
(2)通过正切函数求得OC,即可求得AC,然后通过正切函数求得AB,最后根据∠ADB=∠DAB=∠AOB,从而求得sin∠ADB的值.
解答 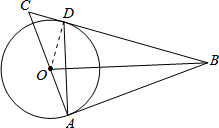 解:(1)连接OD,
解:(1)连接OD,
∵BA=BD,BO⊥AD,
∴∠ABO=∠DBO,
在△ABO和△DBO中
$\left\{\begin{array}{l}{AB=DB}\\{∠ABO=∠DBO}\\{OB=OB}\end{array}\right.$,
∴△ABO≌△DBO(SAS),
∴OD=OA.∠ODB=∠OAB=90°,
∴BD⊥OD,
∴BC是⊙O的切线;
(2)∵在RT△ODC中,CD=$\frac{OD}{tan∠C}$=$\frac{8}{\frac{4}{3}}$=6,
∴OC=10,
∴AC=18
在RT△ABC中,AB=AC•tan∠C=18×$\frac{4}{3}$=24,
∵∠ADB=∠DAB=∠AOB,
∴sin∠ADB=sin∠AOB=$\frac{24}{\sqrt{2{4}^{2}+{8}^{2}}}$=$\frac{3}{10}$$\sqrt{10}$,
点评 本题考查了切线的判定,三角形全等的判定和性质,直角三角函数等,作出辅助线构建全等三角形是解题的关键.

练习册系列答案
相关题目
20.一组数据是4,x,5,10,11共五个数,其平均数为7,则这组数据的众数是( )
| A. | 4 | B. | 5 | C. | 10 | D. | 11 |
5.一次函数y=(m-1)x+m2的图象过点(0,4),且y随x的增大而增大,则m的值为( )
| A. | -2 | B. | 2 | C. | 1 | D. | -2或2 |
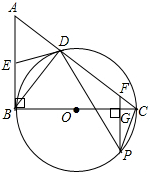 如图,已知,在△ABC中,∠ABC=90°,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
如图,已知,在△ABC中,∠ABC=90°,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.