题目内容
7.点P1(2,y1),P2(4,y2)是一次函数y=(m-2)x+m图象上的两个点,若y1<y2,则m的取值范围是( )| A. | m>0 | B. | m<0 | C. | m>2 | D. | m<2 |
分析 把点P1,P2的坐标分别代入函数解析式,求得相应的y值,然后由已知条件列出关于m的不等式,通过解不等式来求m的取值范围.
解答 解:∵P1(2,y1),P2(4,y2)是一次函数y=(m-2)x+m图象上的两个点,
∴y1=2(m-2)+m=3m-4,y2=4(m-2)+m=5m-8.
又∵y1<y2,
∴3m-4<5m-8,
解得 m>2.
故选:C.
点评 本题考查了一次函数图象上点的坐标特征.此题也可以根据函数的增减性进行解题:由已知条件可以判定m-2>0,由此来求m的取值范围.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
17.已知一次函数y=kx-2,若y随x的增大而减小,则该函数的图象经过哪些象限( )
| A. | 二、三、四 | B. | 一、二、三 | C. | 一、三、四 | D. | 一、二、四 |
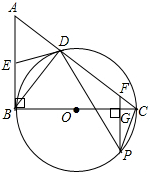 如图,已知,在△ABC中,∠ABC=90°,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
如图,已知,在△ABC中,∠ABC=90°,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F. 看图回答问题:
看图回答问题: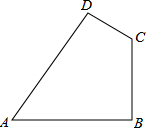 如图,已知在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系并加以证明.
如图,已知在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系并加以证明.