题目内容
6.已知在△ABC中,AB=8,AC=7,BC=5,D点在边AB上,E点在边AC上,如果△ADE与△BCD相似,那么AD=$\frac{39}{8}$.分析 由于∠A≠∠B,∠BDC>∠A,则△ADE与△BCD相似时,可得到∠ADE=∠B,∠A=∠BCD或∠AED=∠B,∠BCD=∠A,于是可判断△BCD∽△BAC,然后利用相似比计算出BD,再计算AB-BD即可.
解答 解: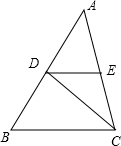 ∵AB=8,AC=7,BC=5,
∵AB=8,AC=7,BC=5,
∴∠A≠∠B,
∵△ADE与△BCD相似,
∴∠ADE=∠B,∠A=∠BCD或∠AED=∠B,∠BCD=∠A,
当∠A=∠BCD时,
∵∠ABC=∠CBD,
∴△BCD∽△BAC,
∴$\frac{BD}{BC}$=$\frac{BC}{AB}$,即$\frac{BD}{5}$=$\frac{5}{8}$,解得BD=$\frac{25}{8}$,
∴AD=AB-BD=8-$\frac{25}{8}$=$\frac{39}{8}$.
故答案为$\frac{39}{8}$.
点评 本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等.也考查了相似三角形的判定.

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
 抛物线y=ax2+bx+c的图象如图所示,则当y≤3时,求x的取值范围.
抛物线y=ax2+bx+c的图象如图所示,则当y≤3时,求x的取值范围.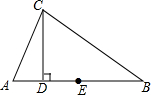 如图,在△ABC中,∠A=2∠B,CD⊥AB,垂足为D,E为AB的中点,若AC=8cm,求DE的长.
如图,在△ABC中,∠A=2∠B,CD⊥AB,垂足为D,E为AB的中点,若AC=8cm,求DE的长.