题目内容
1.(1)计算:(-1)2015+4cos30°-$\sqrt{12}$+|1-$\sqrt{2}$|(2)解不等式组:$\left\{\begin{array}{l}{-2x+1<3x-4}\\{\frac{x}{2}-\frac{x+3}{3}≤1}\end{array}\right.$.
分析 (1)原式第一项利用乘方的意义化简,第二项利用特殊角的三角函数值计算,第三项化为最简二次根式,最后一项利用绝对值的代数意义化简,计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)原式=-1+4×$\frac{\sqrt{3}}{2}$-2$\sqrt{3}$+$\sqrt{2}$-1=$\sqrt{2}$-2;
(2)$\left\{\begin{array}{l}{-2x+1<3x-4①}\\{\frac{x}{2}-\frac{x+3}{3}≤1②}\end{array}\right.$,
由①得:x>1;
由x≤12,
则不等式组的解集为1<x≤12.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.为了“天更蓝”,植树节,人们纷纷响应“植树种绿”的号召,据统计,某市今年参加义务植树活动共有6930余人(次),共计植树18300余株,其中18300用科学记数法表示为( )
| A. | 18.3×103 | B. | 1.83×104 | C. | 0.183×105 | D. | 183×102 |
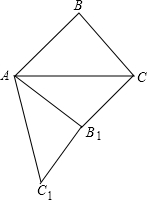 如图,在△ABC中,∠ABC=90°,AB=5,BC=4,将△ABC绕顶点A旋转到△AB1C1的位置(其中点B1对应点B,点C1对应点C),使得B1C∥AB,那么B1C=2.
如图,在△ABC中,∠ABC=90°,AB=5,BC=4,将△ABC绕顶点A旋转到△AB1C1的位置(其中点B1对应点B,点C1对应点C),使得B1C∥AB,那么B1C=2.