题目内容
2.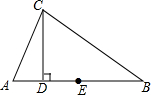 如图,在△ABC中,∠A=2∠B,CD⊥AB,垂足为D,E为AB的中点,若AC=8cm,求DE的长.
如图,在△ABC中,∠A=2∠B,CD⊥AB,垂足为D,E为AB的中点,若AC=8cm,求DE的长.
分析 取AC中点F,连接EF,DF,根据三角形的中位线的性质定理得到EF∥BC,由平行线的性质得到∠FED=∠B,根据直角三角形的性质得到DF=CF=AF=$\frac{1}{2}$AC=4cm,由已知条件推出△DEF是等腰三角形,于是得到结论.
解答 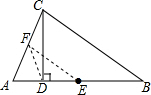 解:取AC中点F,连接EF,DF,
解:取AC中点F,连接EF,DF,
∵E为AB的中点,
∴EF∥BC,
∴∠FED=∠B,
∵CD⊥AB,
∴DF=CF=AF=$\frac{1}{2}$AC=4cm,
∴∠FDA=∠A=2∠B=∠FED+∠EFD=∠B+∠EFD,
∴∠EFD=∠B=∠FED,
∴DE=DF=4cm.
点评 本题考查了等腰三角形的性质,直角三角形的性质,平行线的性质,三角形的中位线的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
相关题目
7.已知A=3m2-7m+5,B=-3m2-7m-7,则B-A一定( )
| A. | 大于0 | B. | 等于-12或-6 | C. | 小于0 | D. | 最大值为12 |
10.多项式x3-x的因式为( )
| A. | x、(x-1) | B. | (x+1) | C. | x2-x | D. | 以上都是 |
12.下面说法中错误的是( )
| A. | 10000万精确到万位 | B. | 2.580精确到千分位 | ||
| C. | 0.0250有3个有效数字 | D. | 17049保留3个有效数字为1.71×104 |
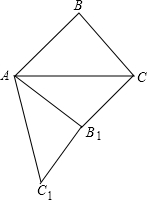 如图,在△ABC中,∠ABC=90°,AB=5,BC=4,将△ABC绕顶点A旋转到△AB1C1的位置(其中点B1对应点B,点C1对应点C),使得B1C∥AB,那么B1C=2.
如图,在△ABC中,∠ABC=90°,AB=5,BC=4,将△ABC绕顶点A旋转到△AB1C1的位置(其中点B1对应点B,点C1对应点C),使得B1C∥AB,那么B1C=2.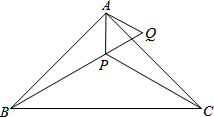 如图,Rt△ABC中,∠BAC=90°,AB=AC,点P是三角形△ABC内部一点,∠ABP=∠ACP,过点A作AQ∥PC交BP的延长线于Q.
如图,Rt△ABC中,∠BAC=90°,AB=AC,点P是三角形△ABC内部一点,∠ABP=∠ACP,过点A作AQ∥PC交BP的延长线于Q.