题目内容
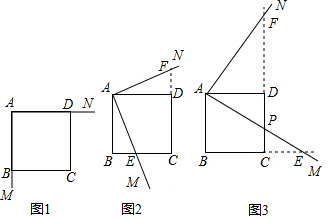
14.如图1,在边长为3的正方形ABCD中,直角∠MAN的两边AM、AN重叠在正方形的两邻边上,现将直角∠MAN绕顶点A旋转.(1)如图2,AM与边长BC相交于点E,AN与边长CD的延长线相交于点F,求证:BE=DF;
(2)如图3,AM、AN与BC、CD的延长线分别相交于点E、F,AM与CD相交于点P,求△APF与△CPE面积的差;
(3)若AM、AN与直线BD分别相交于点G、H,且BG=$\sqrt{2}$,求DH的长.
分析 (1)利用全等三角形的判定和性质证明△ABE与△ADF全等,即可得到BE=DF;
(2)利用①的结论和三角形面积的关系进行证明即可;
(3)由勾股定理求出BD,证明△BEG∽△DAG,得出$\frac{BE}{AD}=\frac{BG}{DG}$=$\frac{1}{2}$,求出$\frac{DF}{AB}$=$\frac{1}{2}$,证明△DFH∽△BAH,得出$\frac{DH}{BH}=\frac{DF}{AB}$=$\frac{1}{2}$,因此DH=$\frac{1}{2}$BH,即可得出DH=BD=3$\sqrt{2}$.
解答 (1)证明:∵四边形ABCD是正方形,
∴AD∥BC,AB∥CD,AB=AD=3,∠BAD=∠B=∠ADC=∠ADF=90°,
∵∠MAN=90°,
∴∠BAE=∠DAF,
∴在△ABE与△ADF中,$\left\{\begin{array}{l}{∠BAE=∠DAF}&{\;}\\{AB=AD}&{\;}\\{∠B=∠ADF}&{\;}\end{array}\right.$,
∴△ABE≌△ADF(ASA),
∴BE=DF;
(2)解:同(1)可证:BE=DF,
连接AC,如图所示:
S△APF-S△CPE=S△ACF-S△ACE
=$\frac{1}{2}$CF•AD-$\frac{1}{2}$CE•AB=$\frac{3}{2}$(CF-CE)
=$\frac{3}{2}$[CD+DF-(BE-BC)]
=$\frac{3}{2}$(CD+BC)=9;
(3)解:∵∠BAD=90°,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=3$\sqrt{2}$,
∵BG=$\sqrt{2}$,
∴DG=BD-BG=2$\sqrt{2}$,
∵AD∥BC,
∴△BEG∽△DAG,
∴$\frac{BE}{AD}=\frac{BG}{DG}$=$\frac{1}{2}$,
∵AB=AD,BE=DF,
∴$\frac{DF}{AB}$=$\frac{1}{2}$,
∵AB∥CD,
∴△DFH∽△BAH,
∴$\frac{DH}{BH}=\frac{DF}{AB}$=$\frac{1}{2}$,
∴DH=$\frac{1}{2}$BH,
∴DH=BD=3$\sqrt{2}$.
点评 此题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质等知识;熟练掌握正方形的性质,证明三角形全等和三角形相似是解决问题的关键.

| A. | m=1 | B. | m=0 | C. | m=3 | D. | m=0或m=3 |
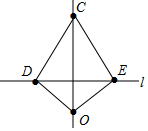 如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D、E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是( )
如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D、E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是( )| A. | 到一个角两边距离相等的点在这个角的角平分线上 | |
| B. | 角平分线上的点到这个角两边的距离相等 | |
| C. | 到线段两端距离相等的点在这条线段的垂直平分线上 | |
| D. | 线段垂直平分线上的点到线段两端的距离相等 |

 如图,在6×6的正方形网格中,每个小正方形顶点叫格点,四边形ABCD的顶点和点Q都在格点上,按要求解答下列问题:
如图,在6×6的正方形网格中,每个小正方形顶点叫格点,四边形ABCD的顶点和点Q都在格点上,按要求解答下列问题: 如图,数轴上的点A、B、C、D、E表示连接的五个整数,若点A、E表示的数分别为x、y,且x+y=2,则点C表示的数为( )
如图,数轴上的点A、B、C、D、E表示连接的五个整数,若点A、E表示的数分别为x、y,且x+y=2,则点C表示的数为( )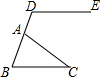 如图,△ABC中,点D在BA的延长线上,DE∥BC,如果∠BAC=65°,∠C=30°,那么∠BDE的度数是95°.
如图,△ABC中,点D在BA的延长线上,DE∥BC,如果∠BAC=65°,∠C=30°,那么∠BDE的度数是95°.