题目内容
13.已知:如图,数轴的单位长度为a,在△ABC中,AB=3a,BC=4a,AC=5a.(1)用直尺和圆规作出△ABC,使点A、C在数轴上(要求:保留痕迹,指出所求);
(2)记△ABC的外接圆的面积为S圆,△ABC的面积为S△ABC,求证:$\frac{{S}_{圆}}{{S}_{△ABC}}$>π.

分析 (1)在数轴上截取线段AC=5a,分别以A、C为圆心,3a、4a为半径画弧,两弧交于点B,△ABC即为所求.
(2)分别求出△ABC外接圆面积,△ABC面积即可解决问题.
解答 解;(1)下图中,△ABC即为所求.
(2)证明:如图2中,
∵AC=5a,AB=3a,BC=4a,
∴AC2=AB2+BC2,
∴∠ABC=90°,
∴△ABC外接圆的直径就是AC,
∴S圆=π•($\frac{AC}{2}$)2=($\frac{5a}{2}$)2π=$\frac{25{a}^{2}}{4}$π.
S△ABC=$\frac{1}{2}$AB•BC=6a2,
∴$\frac{{S}_{圆}}{{S}_{△ABC}}$=$\frac{\frac{25{a}^{2}}{4}π}{6{a}^{2}}$=$\frac{25}{24}$π>π.
点评 本题考查尺规作图、勾股定理逆定理、数轴、三角形外接圆等知识,解题的关键是判断△ABC是直角三角形,属于中考常考题型.

练习册系列答案
相关题目
4. 如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象都经过点A(1,-3),则当x>1时,y1与y2的大小关系为( )
如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象都经过点A(1,-3),则当x>1时,y1与y2的大小关系为( )
 如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象都经过点A(1,-3),则当x>1时,y1与y2的大小关系为( )
如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象都经过点A(1,-3),则当x>1时,y1与y2的大小关系为( )| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法确定 |
8.下列运算正确的是( )
| A. | (x-2)2=x2-4 | B. | (x2)3=x6 | C. | x6÷x3=x2 | D. | x3•x4=x12 |
18.在下列四个角的度数中,一个不等边三角形的最小角度数可以是( )
| A. | 80° | B. | 65° | C. | 60° | D. | 59° |
5.下列命题中,真命题的是( )
| A. | 如果一个四边形两条对角线相等,那么这个四边形是矩形 | |
| B. | 如果一个四边形两条对角线相互垂直,那么这个四边形是菱形 | |
| C. | 如果一个平行四边形两条对角线平分所在的角,那么这个平行四边形是菱形 | |
| D. | 如果一个四边形两条对角线相互垂直平分,那么这个四边形是矩形 |
2.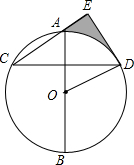 如图,AB是⊙O的直径,弦CD⊥AB,DE⊥CE于E,∠AOD=60°,CD=2$\sqrt{3}$,则S阴影=( )
如图,AB是⊙O的直径,弦CD⊥AB,DE⊥CE于E,∠AOD=60°,CD=2$\sqrt{3}$,则S阴影=( )
 如图,AB是⊙O的直径,弦CD⊥AB,DE⊥CE于E,∠AOD=60°,CD=2$\sqrt{3}$,则S阴影=( )
如图,AB是⊙O的直径,弦CD⊥AB,DE⊥CE于E,∠AOD=60°,CD=2$\sqrt{3}$,则S阴影=( )| A. | $\frac{3\sqrt{3}}{2}$-$\frac{2}{3}$π | B. | $\frac{3\sqrt{3}}{2}$-2π | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{3}}{2}$-π |
 如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED.
如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED. 如图,二次函数y=x2+bx+c的图象交x轴于A、B两点,交y轴于点C,顶点为点P,经过B、C两点的直线为y=-x+3.
如图,二次函数y=x2+bx+c的图象交x轴于A、B两点,交y轴于点C,顶点为点P,经过B、C两点的直线为y=-x+3.