题目内容
2.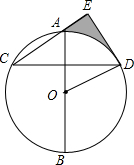 如图,AB是⊙O的直径,弦CD⊥AB,DE⊥CE于E,∠AOD=60°,CD=2$\sqrt{3}$,则S阴影=( )
如图,AB是⊙O的直径,弦CD⊥AB,DE⊥CE于E,∠AOD=60°,CD=2$\sqrt{3}$,则S阴影=( )| A. | $\frac{3\sqrt{3}}{2}$-$\frac{2}{3}$π | B. | $\frac{3\sqrt{3}}{2}$-2π | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{3}}{2}$-π |
分析 连接AD,证出△AOD是等边三角形,得出∠OAD=60°,AD=OD,由垂径定理得出CF=DF=$\frac{1}{2}$CD=$\sqrt{3}$,AC=AD,由三角函数求出AD=OD=2,∠CAD=120°,求出AE=$\frac{1}{2}$AD=1,DE=$\sqrt{3}$AE=$\sqrt{3}$,证出CE∥OD,得出四边形AODE是梯形,阴影部分的面积=梯形的面积-扇形的面积,即可得出结果.
解答 解:连接AD,如图所示:
∵∠AOD=60°,OA=OD,
∴△AOD是等边三角形,
∴∠OAD=60°,AD=OD,
∵AB是⊙O的直径,弦CD⊥AB,
∴CF=DF=$\frac{1}{2}$CD=$\sqrt{3}$,AC=AD,
∴∠ADC=∠ACD=$\frac{1}{2}$∠AOD=30°,∠ODC=90°-60°=30°,
∴AD=OD=$\frac{DF}{sin60°}$=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2,∠CAD=120°,
∴∠DAE=60°,
∵DE⊥CE,
∴∠ADE=30°,
∴AE=$\frac{1}{2}$AD=1,DE=$\sqrt{3}$AE=$\sqrt{3}$,
∵∠ODE=30°+60°=90°,
∴OD⊥DE,
∴CE∥OD,
∴四边形AODE是梯形,
∴S阴影=$\frac{1}{2}$(1+2)×$\sqrt{3}$-$\frac{60π×{2}^{2}}{360}$=$\frac{3\sqrt{3}}{2}$-$\frac{2}{3}$π;
故选:A.
点评 本题考查了圆周角定理、等边三角形的判定与性质、勾股定理、垂径定理、扇形面积的计算、梯形的判定等知识;熟练掌握圆周角定理和垂径定理是解决问题的关键.

| A. | y=-$\frac{1}{x}$ | B. | y=$\frac{1}{x}$ | C. | y=-$\frac{1}{x}$(x>0) | D. | y=$\frac{1}{x}$(x<0) |
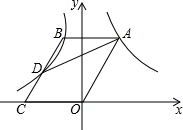 如图,点A在双曲线y=$\frac{6}{x}$(x>0)上,点B在双曲线y=-$\frac{3}{x}$(x<0)上,且AB平行于x轴,BC∥AO交x轴于点C,交双曲线y=-$\frac{3}{x}$(x<0)于点D,连接AD.
如图,点A在双曲线y=$\frac{6}{x}$(x>0)上,点B在双曲线y=-$\frac{3}{x}$(x<0)上,且AB平行于x轴,BC∥AO交x轴于点C,交双曲线y=-$\frac{3}{x}$(x<0)于点D,连接AD.
 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{a}{x}$的图象相交于A,B两点,直线AB与x轴相交于点C,点B的坐标为(-6,m),线段OA=5,E为x轴正半轴上一点,且cos∠AOE=$\frac{3}{5}$.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{a}{x}$的图象相交于A,B两点,直线AB与x轴相交于点C,点B的坐标为(-6,m),线段OA=5,E为x轴正半轴上一点,且cos∠AOE=$\frac{3}{5}$.