题目内容
3．
如图，在Rt△ABC中，∠C=90°，AB边的垂直平分线DE交BC于点E，垂足为D．求证：∠CAB=∠AED．
分析 根据线段垂直平分线的性质得出AE=BE，再由直角三角形的性质即可得出结论．
解答 证明：∵DE是线段AB的垂直平分线，
∴AE=BE，∠ADE=90°，
∴∠EAB=∠B．
在Rt△ABC中，
∵∠C=90°，
∴∠CAB+∠B=90°．
在Rt△ADE中，
∵∠ADE=90°，
∴∠AED+∠EAB=90°，
∴∠CAB=∠AED．
点评 本题考查的是线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
9．一次数学考试中，九年（1）班和（2）班的学生数和平均分如表所示，则这两班平均成绩为82.6分．
| 班级 | 人数 | 平均分 |
| （1）班 | 52 | 85 |
| （2）班 | 48 | 80 |
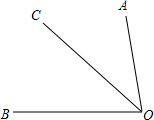如图所示，OC为∠AOB的角平分线，
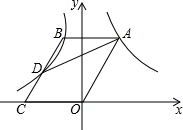如图，点A在双曲线y=$\frac{6}{x}$（x＞0）上，点B在双曲线y=-$\frac{3}{x}$（x＜0）上，且AB平行于x轴，BC∥AO交x轴于点C，交双曲线y=-$\frac{3}{x}$（x＜0）于点D，连接AD．