题目内容
12. 如图,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=9cm,DE=3cm,则BC=12cm.
如图,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=9cm,DE=3cm,则BC=12cm.
分析 过点E作EF⊥BC,垂足为F,延长AD到H,交BC于点H,过点D作DG⊥EF,垂足为G,由直角三角形中30°所对的直角边是斜边的一半可知BF=4.5,DG=1.5,然后由等腰三角形三线合一可知AH⊥BC,BH=CH,然后再证明四边形DGFH是矩形,从而得到FH=GD=1.5,最后根据BC=2BH计算即可.
解答 解;过点E作EF⊥BC,垂足为F,延长AD到H,交BC于点H,过点D作DG⊥EF,垂足为G.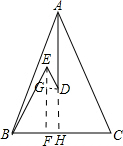
∵EF⊥BC,∠EBF=60°,
∴∠BEF=30°,
∴BF=$\frac{1}{2}BE=\frac{1}{2}×9=4.5$,
∵∠BED=60°,∠BEF=30°,
∴∠DEG=30°.
又∵DG⊥EF,
∴GD=$\frac{1}{2}ED=\frac{1}{2}×3=1.5$,
∵AB=AC,AD平分∠BAC,
∴AH⊥BC,且BH=CH.
∵AH⊥BC,EF⊥BC,DG⊥EF,
∴四边形DGFH是矩形.
∴FH=GD=1.5.
∴BC=2BH=2×(4.5+1.5)=12.
故答案为:12.
点评 本题主要考查的是等腰三角形的性质,含30°直角三角形的性质以及矩形的性质和判定,根据题意构造含30°的直角三角形是解题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
2.已知一次函数y=x+b与反比例函数y=$\frac{4}{x}$的图象相交于点A(1,m).
(1)求一次函数的解析式;
(2)这个一次函数图象沿y轴向下平移4个单位,求平移后的图象与x轴的交点坐标.
(1)求一次函数的解析式;
(2)这个一次函数图象沿y轴向下平移4个单位,求平移后的图象与x轴的交点坐标.
7.下列事件是随机事件的是( )
| A. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| B. | 购买一张福利彩票,中奖 | |
| C. | -2的绝对值小于0 | |
| D. | 在一个仅装着白球和黑球的袋中摸球,摸出红球 |
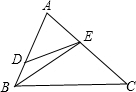 如图,在△ABC中,∠C=45°=∠ADE,BC•AE=24,则S△ABE=6$\sqrt{2}$.
如图,在△ABC中,∠C=45°=∠ADE,BC•AE=24,则S△ABE=6$\sqrt{2}$.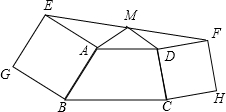 梯形ABCD中,AD∥BC,分别从两腰AB、CD为边作正方形ABGE和CDFH.M为EF中点,求证:MA=MD.
梯形ABCD中,AD∥BC,分别从两腰AB、CD为边作正方形ABGE和CDFH.M为EF中点,求证:MA=MD.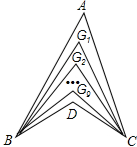 如图,∠ABD,∠ACD的10等分线相交于点G1,G2…G9,若∠BDC=140°,∠BG1C=∠77°,求∠A的度数.
如图,∠ABD,∠ACD的10等分线相交于点G1,G2…G9,若∠BDC=140°,∠BG1C=∠77°,求∠A的度数.