题目内容
2.若3x2-x=1,求9x4+12x3-3x2-7x+2001的值.分析 观察已知3x3-x=1可转化为3x3=x+1,再把9x4+12x3-3x2-7x+2001转化为3x3•3x+3x3•4-3x2-7x+2001,此时将3x3作为一个整体代入x+1,并且代入后通过合并同类项,可将x的各次项系数变为0,最终剩余常数项,使问题得以解决.
解答 解:由3x3-x=1得:3x3=x+1
所以,原式=3x3•3x+3x3•4-3x2-7x+2001
=3x(x+1)+4(x+1)-3x2-7x+2001
=3x2+3x+4x+4-3x2-7x+2001
=2005.
点评 本题考查的是因式分解.解决本题的关键是将3x3作为一个整体出现.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知点P(m+3,m+1)在x轴上,则P点的坐标为( )
| A. | (0,2) | B. | (2,0) | C. | (4,0) | D. | (0,-4) |
 如图,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=9cm,DE=3cm,则BC=12cm.
如图,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=9cm,DE=3cm,则BC=12cm.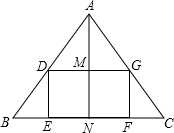 如图,在△ABC中,AB=AC=10,BC=12,矩形DEFG的顶点位于△ABC的边上,设EF=x,SDEFG=y.
如图,在△ABC中,AB=AC=10,BC=12,矩形DEFG的顶点位于△ABC的边上,设EF=x,SDEFG=y.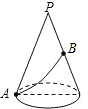 如图,一个圆锥的母线长为10cm,底面半径为5cm,在圆锥的底面边缘上一点A处有一只蚂蚁,想吃到点A相对的母线的中点B处的一粒砂糖,这只蚂蚁从点A出发,沿着曲面爬到点B,最短路线的长是多少?
如图,一个圆锥的母线长为10cm,底面半径为5cm,在圆锥的底面边缘上一点A处有一只蚂蚁,想吃到点A相对的母线的中点B处的一粒砂糖,这只蚂蚁从点A出发,沿着曲面爬到点B,最短路线的长是多少?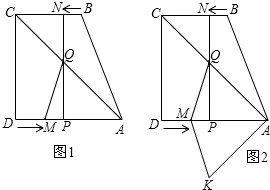
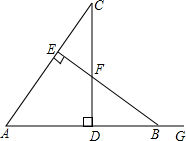 如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.
如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.