题目内容
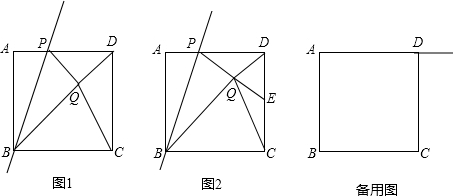
 已知在正方形ABCD中,F在对角线AC上,BF⊥FE,且AF=CE=2,求正方形ABCD的面积.
已知在正方形ABCD中,F在对角线AC上,BF⊥FE,且AF=CE=2,求正方形ABCD的面积.考点:全等三角形的判定与性质,等腰三角形的判定与性质,正方形的性质
专题:
分析:过点F作FH⊥CD于D,作MN∥AN分别交BC、AD于M、N,根据正方形的性质可得FH=FM,△ANH是等腰直角三角形,四边形FHDN是矩形,然后求出AN=BM=FN=DH=
,再根据同角的余角相等求出∠BFM=∠EFH,利用“角角边”证明△BFM和△EFH全等,根据全等三角形对应边相等可得EH=BM,再求出CD,然后根据正方形的面积公式列式计算即可得解.
| 2 |
解答: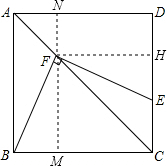 解:如图,过点F作FH⊥CD于D,作MN∥AN分别交BC、AD于M、N,
解:如图,过点F作FH⊥CD于D,作MN∥AN分别交BC、AD于M、N,
∵点F是正方形ABCD对角线上的点,
∴FH=FM,△ANH是等腰直角三角形,四边形FHDN是矩形,
∵AF=2,
∴AN=BM=FN=DH=
,
∵BF⊥FE,
∴∠BFM+∠CFM=90°,
又∵∠EFH+∠EFM=90°,
∴∠BFM=∠EFH,
在△BFM和△EFH中,
,
∴△BFM≌△EFH(AAS),
∴EH=BM,
∴CD=DH+EH+CE=
+
+2=2+2
,
∴正方形ABCD的面积=(2+2
)2=12+8
.
 解:如图,过点F作FH⊥CD于D,作MN∥AN分别交BC、AD于M、N,
解:如图,过点F作FH⊥CD于D,作MN∥AN分别交BC、AD于M、N,∵点F是正方形ABCD对角线上的点,
∴FH=FM,△ANH是等腰直角三角形,四边形FHDN是矩形,
∵AF=2,
∴AN=BM=FN=DH=
| 2 |
∵BF⊥FE,
∴∠BFM+∠CFM=90°,
又∵∠EFH+∠EFM=90°,
∴∠BFM=∠EFH,
在△BFM和△EFH中,
|
∴△BFM≌△EFH(AAS),
∴EH=BM,
∴CD=DH+EH+CE=
| 2 |
| 2 |
| 2 |
∴正方形ABCD的面积=(2+2
| 2 |
| 2 |
点评:本题考查了全等三角形的判定与性质,正方形的性质,等腰直角三角形的判断与性质,熟记各性质并作辅助线构造出矩形和全等三角形是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 如图,在锐角△ABC中,探究
如图,在锐角△ABC中,探究 已知:在ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于H,且BH=AC,证明:DH=DC.
已知:在ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于H,且BH=AC,证明:DH=DC.