题目内容
5.如果有4个不同的正整数a、b、c、d满足(2016-a)(2016-b)(2016-c)(2016-d)=9,那么a+b+c+d的值为( )| A. | 0 | B. | 9 | C. | 8048 | D. | 8064 |
分析 根据a、b、c、d是四个不同的正整数可知四个括号内的值分别是:±1,±3,据此可得出结论.
解答 解:∵a、b、c、d是四个不同的正整数,
∴四个括号内的值分别是:±1,±3,
∴2016+1=2017,2016-1=2015,2015+3=2019,2016-3=2013,
∴a+b+c+d=2017+2015+2019+2013=8064.
故选D.
点评 本题考查的是有理数的混合运算,根据题意得出四个括号中的数是解答此题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
15.2016年国家公务员考试报名人数约为1390000,将1390000用科学记数法表示,表示正确的为( )
| A. | 1.39×105 | B. | 1.39×106 | C. | 13.9×105 | D. | 13.9×106 |
14.把分式方程$\frac{x}{{x}^{2}-4}$+2=$\frac{2x}{x-2}$化为整式方程,得( )
| A. | x+2=2x(x+2) | B. | x+2(x2-4)=2x(x+2) | C. | x+2(x-2)=2x(x-2) | D. | x+2(x2-4)=2x(x-2) |
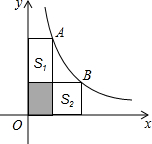 A、B两点在双曲线y=$\frac{5}{x}$上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=8.
A、B两点在双曲线y=$\frac{5}{x}$上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=8.