题目内容
4.在△PMN中,PM=PN,AB是线段PM的对称轴,且AB分别交线段PM于A,交线段PN于B,若△PMN的周长为60厘米,△BMN的周长为36厘米,则MN的长为( )| A. | 6厘米 | B. | 12厘米 | C. | 18厘米 | D. | 24厘米 |
分析 先根据线段垂直平分线的性质得出PB=MB,PA=MA,再根据△PMN的周长为60cm,△BMN的周长为36cm得出PM的长,进而可得出结论.
解答  解:如图所示,∵AB是线段PM的对称轴,
解:如图所示,∵AB是线段PM的对称轴,
∴PB=MB,PA=MA,
∵△PMN的周长为60cm,△BMN的周长为36cm,
∴PM=60-36=24cm=PN,
∴MN=60-24×2=12cm.
故选B.
点评 本题考查的是轴对称的性质以及线段垂直平分线的性质,熟知线段垂直平分线上的点到线段两端的距离相等是解答此题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
19.下列运算正确的是( )
| A. | x4+x4=2x8 | B. | x6÷x2=x3 | C. | (-x5)2=x10 | D. | xm•xn=xmn |
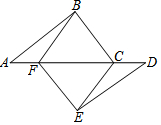 如图,点A、F、C、D在同一条直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠BAD=∠ADE,AF=DC.求证:四边形BCEF是平行四边形.
如图,点A、F、C、D在同一条直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠BAD=∠ADE,AF=DC.求证:四边形BCEF是平行四边形.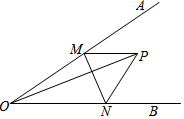 如图,已知∠AOB=45°,∠AOB内有一点P,OP=6$\sqrt{2}$,M为射线OA上一动点,N为射线OB上一动点,则PM+MN+PN的最小值为12.
如图,已知∠AOB=45°,∠AOB内有一点P,OP=6$\sqrt{2}$,M为射线OA上一动点,N为射线OB上一动点,则PM+MN+PN的最小值为12.