题目内容
9.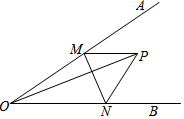 如图,已知∠AOB=45°,∠AOB内有一点P,OP=6$\sqrt{2}$,M为射线OA上一动点,N为射线OB上一动点,则PM+MN+PN的最小值为12.
如图,已知∠AOB=45°,∠AOB内有一点P,OP=6$\sqrt{2}$,M为射线OA上一动点,N为射线OB上一动点,则PM+MN+PN的最小值为12.
分析 首先分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,易得△OCD是等腰直角三角形,且此时CD的长即为PN+MN+PN的最小值,继而求得答案.
解答 解:如图所示:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN, ∵点P关于OA的对称点为C,关于OB的对称点为D,
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PM=CM,OP=OC,∠COA=∠POA;
∵点P关于OB的对称点为D,
∴PN=DN,OP=OD,∠DOB=∠POB,
∴OC=OD=OP=6$\sqrt{2}$,∠COD=2∠AOB=2×45°=90°,
∴CD=$\sqrt{O{C}^{2}+O{D}^{2}}$=12,
∵PN+PM+MN的最小值是12.
故答案为:12.
点评 本题考查了轴对称的性质、最短路线问题以及等腰三角形的判定与性质.注意准确确定点M,N的位置是关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
19.某超市在春节期间对顾客实行优惠,规定如下:
(1)刘老师一次性购物600元,求他实际付款多少元?
(2)若顾客在该超市一次性购物x元(x≥500),实际付款y元,请求出用含x的代数式表示y的式子.
(3)如果刘老师两次购物贷款合计820元,第一次购物的贷款为a元(200<a<300),用含a的代数式表示:两次购物刘老师实际多少元?
| 一次性购物 | 优惠方法 |
| 少于200元 | 不予优惠 |
| 低于500元但不低于200元 | 九折优惠 |
| 500元或超过500元 | 其中500元部分给予九折优惠,超过500元部分给予八折优惠 |
(2)若顾客在该超市一次性购物x元(x≥500),实际付款y元,请求出用含x的代数式表示y的式子.
(3)如果刘老师两次购物贷款合计820元,第一次购物的贷款为a元(200<a<300),用含a的代数式表示:两次购物刘老师实际多少元?
17.计算(ab2)4的结果,正确的是( )
| A. | a4b8 | B. | a4b6 | C. | ab8 | D. | ab6 |
4.在△PMN中,PM=PN,AB是线段PM的对称轴,且AB分别交线段PM于A,交线段PN于B,若△PMN的周长为60厘米,△BMN的周长为36厘米,则MN的长为( )
| A. | 6厘米 | B. | 12厘米 | C. | 18厘米 | D. | 24厘米 |
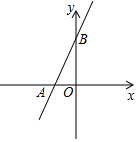 已知直线L经过点A(-2,0),B(0,3)
已知直线L经过点A(-2,0),B(0,3)