题目内容
12. 如图,在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
如图,在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
分析 根据平行四边形的性质,可得AB与CD的关系,根据平行四边形的判定,可得BFDE是平行四边形,再根据矩形的判定,可得四边形BFDE是矩形;根据平行线的性质,可得∠DFA=∠FAB,根据等腰三角形的判定与性质,可得∠DAF=∠DFA,根据角平分线的判定,可得答案.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
∴AB∥DC,
∴∠DFA=∠FAB.
在Rt△BCF中,由勾股定理,得
BC=$\sqrt{F{C}^{2}+F{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴AD=BC=DF=5,
∴∠DAF=∠DFA,
∴∠DAF=∠FAB,
即AF平分∠DAB.
点评 本题考查了平行四边形的性质,利用了平行四边形的性质,矩形的判定,等腰三角形的判定与性质,利用等腰三角形的判定与性质得出∠DAF=∠DFA是解题关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
2. 如图,AD、BE分别是等边△ABC边BC、AC上的中线,AD、BE相交于点O,则∠AOB的度数为( )
如图,AD、BE分别是等边△ABC边BC、AC上的中线,AD、BE相交于点O,则∠AOB的度数为( )
 如图,AD、BE分别是等边△ABC边BC、AC上的中线,AD、BE相交于点O,则∠AOB的度数为( )
如图,AD、BE分别是等边△ABC边BC、AC上的中线,AD、BE相交于点O,则∠AOB的度数为( )| A. | 120° | B. | 105° | C. | 130° | D. | 135° |
3. 一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形,在满足条件的所有分割中.若知道九个小矩形中n个小矩形的周长,就一定能算出这个大矩形的面积,则n的最小值是( )
一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形,在满足条件的所有分割中.若知道九个小矩形中n个小矩形的周长,就一定能算出这个大矩形的面积,则n的最小值是( )
 一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形,在满足条件的所有分割中.若知道九个小矩形中n个小矩形的周长,就一定能算出这个大矩形的面积,则n的最小值是( )
一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形,在满足条件的所有分割中.若知道九个小矩形中n个小矩形的周长,就一定能算出这个大矩形的面积,则n的最小值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
20.函数y=$\frac{x-5}{\sqrt{x-1}}$自变量x的取值范围是( )
| A. | x>1 | B. | x≥1 | C. | x>-2 | D. | x≥-2 |
7.下列说法不正确的是( )
| A. | x=-2是不等式-2x>1的一个解 | B. | x=-2是不等式-2x>1的一个解集 | ||
| C. | x-7>2x+8与x<15的解集不相同 | D. | x<-3与-7x>21的解集相同 |
4.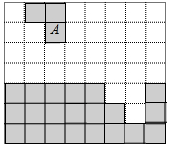 如图,若图形A经过平移与下方图形拼成一个长方形,则正确的平移方式是( )
如图,若图形A经过平移与下方图形拼成一个长方形,则正确的平移方式是( )
 如图,若图形A经过平移与下方图形拼成一个长方形,则正确的平移方式是( )
如图,若图形A经过平移与下方图形拼成一个长方形,则正确的平移方式是( )| A. | 向右平移4格,再向下平移4格 | B. | 向右平移6格,再向下平移5格 | ||
| C. | 向右平移4格,再向下平移3格 | D. | 向右平移5格,再向下平移3格 |
 如图,矩形ABCD中,AB=6,AD=8,P,E分别是线段AC、BC上的点,且四边形PEFD为矩形.
如图,矩形ABCD中,AB=6,AD=8,P,E分别是线段AC、BC上的点,且四边形PEFD为矩形.