题目内容
17.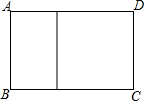 如图,用长120cm的木条制成如图形状的矩形框(矩形框中间有一横档).设矩形框的宽AB为x(cm),所围成的面积为S(cm2).
如图,用长120cm的木条制成如图形状的矩形框(矩形框中间有一横档).设矩形框的宽AB为x(cm),所围成的面积为S(cm2).(1)求S关于x的函数表达解析式和自变量x的取值范围;
(2)要使矩形框的面积为594cm2,则AB的长为多少;
(3)能围成面积比594cm2更大的矩形框吗?如果能,求出最大面积,并说明围法;如果不能,请说明理由.
分析 (1)由AB=x且木条的总长为120cm得出BC=$\frac{120-3x}{2}$cm,根据矩形的面积公式可得函数解析式,由AB>0且BC>0可得x的范围;
(2)根据(1)中函数解析式,令S=594列出关于x的方程求解可得;
(3)将(1)中函数解析式配方成顶点式,根据二次函数的性质可得最值.
解答 解:(1)当AB=xcm时,BC=$\frac{120-3x}{2}$cm,
∴S=x•$\frac{120-3x}{2}$=-$\frac{3}{2}$x2+60x,
∵$\frac{120-3x}{2}$>0,且x>0,
∴0<x<40;
(2)根据题意,得:-$\frac{3}{2}$x2+60x=594,
解得:x=22或x=18,
答:要使矩形框的面积为594cm2,则AB的长为22cm或18cm;
(3)∵S=-$\frac{3}{2}$x2+60x=-$\frac{3}{2}$(x-20)2+600,
∴当x=20时,S取得最大值,最大值为600cm2,
故能围成面积比594cm2更大的矩形框,当AB=20cm、BC=30cm时,窗框的面积最大,最大面积为600cm2.
点评 本题主要考查二次函数的应用与一元二次方程的应用,根据题意得出BC的长是解题的根本,由矩形的面积公式得出函数解析式及一元二次方程是解题的关键.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
12. 如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=135°,则∠4的度数为( )
如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=135°,则∠4的度数为( )
 如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=135°,则∠4的度数为( )
如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=135°,则∠4的度数为( )| A. | 55° | B. | 65° | C. | 135° | D. | 45° |
7.已知一组正数a,b,c,d的平均数为2,则a+2,b+2,c+2,d+2的平均数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
 如图,已知等腰直角△ABC的直角边长与正方形DEFG的边长均为8cm,EF与AC在同一条直线上,开始时点A与点F重合,让△ABC向左移动,运动速度为1cm/s,最后点A与点E重合.
如图,已知等腰直角△ABC的直角边长与正方形DEFG的边长均为8cm,EF与AC在同一条直线上,开始时点A与点F重合,让△ABC向左移动,运动速度为1cm/s,最后点A与点E重合.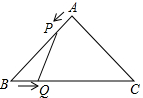 如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t s,四边形APQC的面积为y cm2.
如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t s,四边形APQC的面积为y cm2. 如图,AO=BO=2,∠AOB=90°,△A′、C、D分别与点A重合,在边BO上、在边BO的延长线上,且A′C=A′D=$\sqrt{5}$,将△A′CD沿射线OB平移,设平移距离为x(其中0<x<3),平移后的图形与△ABO重叠部分的面积为S.
如图,AO=BO=2,∠AOB=90°,△A′、C、D分别与点A重合,在边BO上、在边BO的延长线上,且A′C=A′D=$\sqrt{5}$,将△A′CD沿射线OB平移,设平移距离为x(其中0<x<3),平移后的图形与△ABO重叠部分的面积为S.
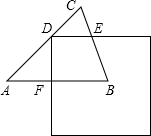 如图,在△ABC中,AB=AC=1,∠A=60°,边长为1的正方形的一个顶点D在边AC上,与△ABC另两边分别交于点E、F,DE∥AB,将正方形平移,使点D保持在AC上(D不与A重合),设AF=x,正方形与△ABC重叠部分的面积为y.
如图,在△ABC中,AB=AC=1,∠A=60°,边长为1的正方形的一个顶点D在边AC上,与△ABC另两边分别交于点E、F,DE∥AB,将正方形平移,使点D保持在AC上(D不与A重合),设AF=x,正方形与△ABC重叠部分的面积为y.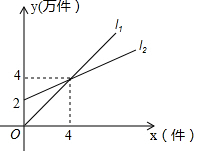 如图,l1表示某产品一天的销售收入与销售量的关系;l2表示该产品一天的销售成本与销售量的关系.则销售收入y1与销售量之间的函数关系式y1=x,销售成本y2与销售量之间的函数关系式y2=$\frac{1}{2}$x+2,当一天的销售量超过x>4时,生产该产品才能获利.(提示:利润=收入-成本)
如图,l1表示某产品一天的销售收入与销售量的关系;l2表示该产品一天的销售成本与销售量的关系.则销售收入y1与销售量之间的函数关系式y1=x,销售成本y2与销售量之间的函数关系式y2=$\frac{1}{2}$x+2,当一天的销售量超过x>4时,生产该产品才能获利.(提示:利润=收入-成本)