Question

17．如果等腰三角形底角的角平分线的长度恰好是底边上的高的2倍，试求顶角的度教．

Answer 1

分析 如图，AB=AC，BD是△ABC的角平分线，BE是高，BD=2BE，AF⊥BC于F，设∠CBE=∠CAF=∠BAF=x，则∠DBC=x-60°，列出方程即可解决问题．

解答 解：如图，AB=AC，BD是△ABC的角平分线，BE是高，BD=2BE，AF⊥BC于F，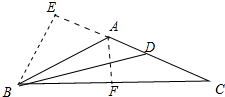

在Rt△BDE中，∵BD=2BE，
∴∠BDE=30°，∠DBE=60°，
∵∠C+∠CAF=90°，∠C+∠CBE=90°，
∴∠CBE=∠CAF=∠BAF，设∠CBE=∠CAF=∠BAF=x，则∠DBC=x-60°，
∴2x+4（x-60°）=180°，
∴x=70°，
∴∠BAC=2x=140°，
∴等腰三角形顶角的度数为140°．

点评 本题考查角平分线的性质、等腰三角形的性质、三角形内角和定理等知识，解题的关键是灵活应用知识知识解决问题，属于中考常考题型．