题目内容
18.经市场调查,某种商品在第x天(1≤x≤90)的售价与销量的相关信息如下表:| 时间x(天) | 1≤x≤60 | 60≤x≤90 |
| 售价(元/件) | x+40 | 100 |
| 每天销量(件) | 200-2x | |
(I)分别求出当1≤x<60和60≤x≤90时,该商品每天利润y与x之间的函数表达式.
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少元?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
分析 (1)根据单价乘以数量,可得利润,可得答案;
(2)根据分段函数的性质,可分别得出最大值,根据有理数的比较,可得答案;
(3)根据二次函数值大于或等于4800,一次函数值大于或等于48000,可得不等式,根据解不等式组,可得答案.
解答 解:(1)当1≤x<60时,y=(200-2x)(x+40-30)=-2x2+180x+2000,
当60≤x≤90时,
y=(200-2x)(100-30)=-140x+14000;
(2)当1≤x<60时,二次函数开口向下,二次函数对称轴为x=45,
当x=45时,y最大=-2×452+180×45+2000=6050,
当60≤x≤90时,y随x的增大而减小,
当x=60时,y最大=6000,
综上所述,该商品第45天时,当天销售利润最大,最大利润是6050元;
(3)当1≤x<60时,y=-2x2+180x+2000≥4800,解得20≤x≤70,
因此利润不低于4800元的天数是20≤x<50,共30天;
当60≤x≤90时,y=-140x+14000≥4800,解得x≤80,
因此利润不低于4800元的天数是60≤x≤80,共21天,
所以该商品在销售过程中,共51天每天销售利润不低于4800元.
点评 本题考查了二次函数的应用,利用单价乘以数量求函数解析式,利用了函数的性质求最值.

练习册系列答案
相关题目
8.下列关于菱形、矩形的说法正确的是( )
| A. | 菱形的对角线相等且互相平分 | B. | 矩形的对角线相等且互相平分 | ||
| C. | 对角线互相垂直的四边形是菱形 | D. | 对角线相等的四边形是矩形 |
 小明在他家里的时钟上安装了一个电脑软件,他设定当钟声在n点钟响起后,下一次则在(3n-1)小时后响起,例如钟声第一次在3点钟响起,那么第2次在(3×3-1=8)小时后,也就是11点响起,第3次在(3×11-1=32)小时后,即7点响起,以此类推…;现在第1次钟声响起时为2点钟,那么第3次响起时为3点,第2017次响起时为11点(如图钟表,时间为12小时制).
小明在他家里的时钟上安装了一个电脑软件,他设定当钟声在n点钟响起后,下一次则在(3n-1)小时后响起,例如钟声第一次在3点钟响起,那么第2次在(3×3-1=8)小时后,也就是11点响起,第3次在(3×11-1=32)小时后,即7点响起,以此类推…;现在第1次钟声响起时为2点钟,那么第3次响起时为3点,第2017次响起时为11点(如图钟表,时间为12小时制).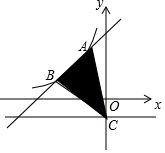 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x<0)的图象交于A(-1,3),B(-3,n)两点,直线y=-1与y轴交于点C.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x<0)的图象交于A(-1,3),B(-3,n)两点,直线y=-1与y轴交于点C.