题目内容
6. 如图,P为正方形ABCD边BC的中点,DE⊥AP于点E,F为AP上一点,AE=EF,∠CDF的平分线交AP的延长线于点G,连接CG,下列结论:①DE=2AE;②AG⊥CG;③△DEG为等腰直角三角形;④$\frac{CG}{AG}=\frac{1}{3}$.其中正确结论的个数是( )
如图,P为正方形ABCD边BC的中点,DE⊥AP于点E,F为AP上一点,AE=EF,∠CDF的平分线交AP的延长线于点G,连接CG,下列结论:①DE=2AE;②AG⊥CG;③△DEG为等腰直角三角形;④$\frac{CG}{AG}=\frac{1}{3}$.其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由四边形ABCD是正方形,于是得到∠BAD=∠B=90°,AB=BC,根据余角的性质得到∠BAE=ADE,推出△ABP∽△ADE,根据相似三角形的性质得到$\frac{AB}{BP}=\frac{DE}{AE}$,由P为正方形ABCD边BC的中点,于是得到BP=$\frac{1}{2}$BC=$\frac{1}{2}$AB,求得DE=2AE;故①正确;通过△FDG≌△CDG,得到∠DFG=∠DCG,根据邻补角的定义得到∠AFD+∠DFG=180°,推出A,G,C,D四点共圆于是得到∠AGC=90°,AG⊥CG;故②正确;根据全等三角形的性质得到∠AGD=∠CGD=$\frac{1}{2}∠AGC=45°$,求出∠EDG=45°,得到△DEG为等腰直角三角形;故③正确;等量代换得到FG=EF=AE=$\frac{1}{3}$AG,根据全等三角形的性质得到CG=FG=$\frac{1}{3}$AG,于是得到$\frac{CG}{AG}=\frac{1}{3}$;故④正确.
解答 解:∵四边形ABCD是正方形,
∴∠BAD=∠B=90°,AB=BC,
∵DE⊥AP于点E,
∴∠AED=90°,
∴∠BAE+∠DAE=∠DAE+∠ADE=90°,
∴∠BAE=ADE,
∴△ABP∽△ADE,
∴$\frac{AB}{BP}=\frac{DE}{AE}$,
∵P为正方形ABCD边BC的中点,
∴BP=$\frac{1}{2}$BC=$\frac{1}{2}$AB,
∴$\frac{AB}{BP}=\frac{DE}{AE}$=2,
∴DE=2AE;故①正确;
∵AE=EF,
∴AD=DF,
∴∠DAE=∠DFE,
∵DG平分∠FDC,
∴∠FDG=∠CDG,
在△FDG与△CDG中,
$\left\{\begin{array}{l}{DF=DC}\\{∠FDG=∠CDG}\\{DG=DG}\end{array}\right.$,
∴△FDG≌△CDG,
∴∠DFG=∠DCG,
∵∠AFD+∠DFG=180°,
∴∠DAF+∠DCG=180°,
∴A,G,C,D四点共圆,
∴∠ADC+∠AGC=180°,
∵∠ADC=90°,
∴∠AGC=90°,AG⊥CG;故②正确;
∵△FDG≌△CDG,
∴∠AGD=∠CGD=$\frac{1}{2}∠AGC=45°$,
∴∠EDG=45°,
∴△DEG为等腰直角三角形;故③正确;
∴EG=DE=2AE=2EF,
∴FG=EF=AE=$\frac{1}{3}$AG,
∵△FDG≌△CDG,
∴CG=FG=$\frac{1}{3}$AG,
∴$\frac{CG}{AG}=\frac{1}{3}$;故④正确.
故选D.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,正方形的性质,等腰直角三角形的判定和性质,角平分线的定义,熟练掌握全等三角形的判定定理是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 2460(1-x)2=1800 | B. | 1800(1+x)2=2460 | ||
| C. | 1800(1-x)2=2460 | D. | 1800+1800(1+x)+1800(1+x)2=2460 |
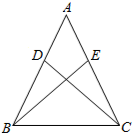 已知:如图,在△ABC中,AB=AC,在AB、AC上分别截取相等的两条线段AD、AE,并连结BE、CD.求证:△ADC≌△AEB.
已知:如图,在△ABC中,AB=AC,在AB、AC上分别截取相等的两条线段AD、AE,并连结BE、CD.求证:△ADC≌△AEB.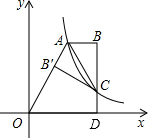 如图,双曲线$y=\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则
如图,双曲线$y=\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则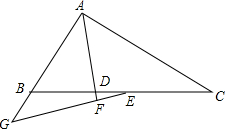 已知,△ABC中,AD是角平分线,点E在BC上,EF⊥AD交AD、AB于F、G.
已知,△ABC中,AD是角平分线,点E在BC上,EF⊥AD交AD、AB于F、G.



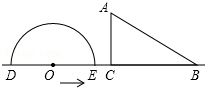 如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧.
如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧. 如图,A、B分别为数轴上两点,A点对应的数为-20,B点对应的数为80.
如图,A、B分别为数轴上两点,A点对应的数为-20,B点对应的数为80.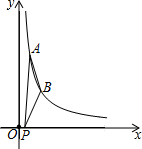 如图,双曲线$y=\frac{k}{x}$(x>0)经过点A(1,6)、点B(2,n),点P的坐标为(t,0),且-1≤t<3,则△PAB的最大面积为6.
如图,双曲线$y=\frac{k}{x}$(x>0)经过点A(1,6)、点B(2,n),点P的坐标为(t,0),且-1≤t<3,则△PAB的最大面积为6.