题目内容
9.解不等式组$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x}\\{1-2(x-1)<4-x}\end{array}\right.$,并写出不等式组的整数解.分析 先求出两个不等式的解集,再求其公共解.
解答 解:$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x①}\\{1-2(x-1)<4-x②}\end{array}\right.$
由①得:x≤3,
由②得:x>-1,)
∴不等式组的解集为:-1<x≤3;
∴不等式组的整数解:0,1,2,3.
点评 本题主要考查不等式组的解法,及根据未知数的范围确定它所满足的特殊条件的值.一般方法是先解不等式组,再根据解集求出特殊值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.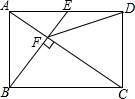 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有( )
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
4.已知正整数中a、b、c,c=7且a<b<c,则以a、b、c为三边长的三角形共有( )
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
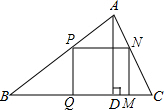 如图,△ABC是一块锐角三角形余料,边BC=12cm,高AD=8cm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.若这个矩形的长是宽的2倍,求矩形的长和宽.
如图,△ABC是一块锐角三角形余料,边BC=12cm,高AD=8cm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.若这个矩形的长是宽的2倍,求矩形的长和宽.