题目内容
11.阅读材料:13+23=1+8=9,而(1+2)2=9,所以13+23=(1+2)2,13+23+33=36,而(1+2+3)2=36所以13+23+33=(1+2+3)2,13+23+33+43=100,而(1+2+3+4)2=100,所以13+23+33=(1+2+3)2,13+23+33+43=100,而(1+2+3+4)2=100,所以13+23+33+43=(1+2+3+4)2,则 13+23+33+43+53=1+2+3+4+52=225.求(1)13+23+33+…+n3=(1+2+3+…+n)2=[$\frac{n(n+1)}{2}$]2(n为整数);
(2)113+123+133+143+153.
分析 观察前4组式子,发现规律,可设13+23+33+43+…+n3=t,则(1+2+3+4+…+n)2=t,从而可得结论.
解答 解:根据以上规律可得13+23+33+43+53=(1+2+3+4+5)2=225;
(1)13+23+33+…+n3=(1+2+3+…+n)2=($\frac{n(n+1)}{2}$)2;
(2)113+123+133+143+153
=(1+2+3+…+15)2-(1+2+3+…+10)2
=${(\frac{15×16}{2})^2}-{(\frac{10×11}{2})^2}$
=11375.
故答案为:1+2+3+4+5;225;(1)1+2+3+…+n;$\frac{n(n+1)}{2}$.
点评 本题主要考查了归纳推理,解题的关键找出其规律,同时考查了运算求解的能力的能力,属于基础题.

练习册系列答案
相关题目
1.若k>0,点P(-k,k)在第( )象限.
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2. 如图,在同一平面内,两条平行的高速l1和l2间有一条“z”型道路连通,其中AB段与高速公路l1成30°角,CD与l2成40°的角,∠ABC=90°,则∠BCD的度数为( )
如图,在同一平面内,两条平行的高速l1和l2间有一条“z”型道路连通,其中AB段与高速公路l1成30°角,CD与l2成40°的角,∠ABC=90°,则∠BCD的度数为( )
 如图,在同一平面内,两条平行的高速l1和l2间有一条“z”型道路连通,其中AB段与高速公路l1成30°角,CD与l2成40°的角,∠ABC=90°,则∠BCD的度数为( )
如图,在同一平面内,两条平行的高速l1和l2间有一条“z”型道路连通,其中AB段与高速公路l1成30°角,CD与l2成40°的角,∠ABC=90°,则∠BCD的度数为( )| A. | 70° | B. | 90° | C. | 100° | D. | 110° |
6.下列多项式能用平方差公式因式分解的是( )
| A. | 2x2-y2 | B. | x2-x-2 | C. | a2-4a+4 | D. | -1+a2 |
 如图,AD∥BC,∠α=50°,∠B=∠C,请求出∠B,∠C,∠D的度数.
如图,AD∥BC,∠α=50°,∠B=∠C,请求出∠B,∠C,∠D的度数.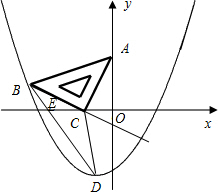 如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点A的坐标为(0,2),点B在抛物线y=ax2+ax-2上.
如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点A的坐标为(0,2),点B在抛物线y=ax2+ax-2上.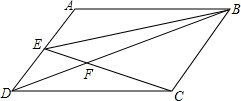 如图,在?ABCD中,点E是AD中点.
如图,在?ABCD中,点E是AD中点.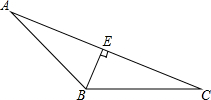 如图,在△ABC中,BE⊥AC,BC=5cm,AC=8cm,BE=3cm,
如图,在△ABC中,BE⊥AC,BC=5cm,AC=8cm,BE=3cm,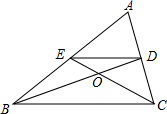 如图,在△ABC中,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O,则$\frac{OB}{OD}$=2.
如图,在△ABC中,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O,则$\frac{OB}{OD}$=2.