题目内容
3.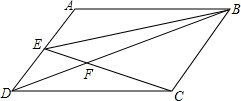 如图,在?ABCD中,点E是AD中点.
如图,在?ABCD中,点E是AD中点.(1)求△DEF与△CBF的周长比;
(2)如果S△EFB=9cm2,求S△CFD和S?ABCD的值.
分析 (1)由四边形ABCD是平行四边形,E是AD的中点,可得△DEF∽△BCF,DE:BC=1:2,然后根据相似三角形周长的比等于相似比,即可求得答案.
(2)由于AD∥BC,根据平行线间的距离相等可知S△DEB=S△DEC,所以S△CFD=S△EFB=9cm2,因为△DEF∽△BCF,且$\frac{DE}{BC}=\frac{DF}{FB}=\frac{1}{2}$,所以$\frac{DF}{BD}=\frac{1}{3}$,所以$\frac{S△CFD}{S△BDC}=\frac{1}{3}$,于是S△BCD=27cm2,S?ABCD=2S△BCD=54cm2.
解答 解:(1)∵四边形ABCD是平行四边形,
∴BC=AD,AD∥BC,
∵E是AD的中点,
∴DE=$\frac{1}{2}$AD,
∴DE:BC=1:2,
∵AD∥BC,
∴△DEF∽△BCF,
∴C△DEF:C△BCF=1:2.
(2)∵AD∥BC,
∴S△DEB=S△DEC,
∴S△CFD=S△EFB=9cm2,
由(1)知:△BEF∽△DAF,且$\frac{DE}{BC}=\frac{DF}{FB}=\frac{1}{2}$,
∴$\frac{DF}{BD}=\frac{1}{3}$,
∴$\frac{S△CFD}{S△BDC}=\frac{1}{3}$,
∴S△BCD=3S△CFD=27cm2,
∴S?ABCD=2S△BCD=54cm2.
点评 此题考查了相似三角形的判定与性质与平行四边形的性质,此题难度不大,解题的关键是掌握相似三角形周长的比等于相似比的定理的应用,注意数形结合思想的应用.

练习册系列答案
相关题目
15.下列各式不能用平方差公式法分解因式的是( )
| A. | x2-4 | B. | -x2-y2 | C. | m2n2-1 | D. | a2-4b2 |
13.计算(-1)0的结果为( )
| A. | 1 | B. | -1 | C. | 0 | D. | 无意义 |