题目内容
20.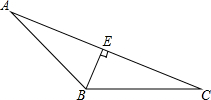 如图,在△ABC中,BE⊥AC,BC=5cm,AC=8cm,BE=3cm,
如图,在△ABC中,BE⊥AC,BC=5cm,AC=8cm,BE=3cm,(1)求△ABC的面积;
(2)画出△ABC中的BC边上的高AD,并求出AD的值.
分析 (1)根据三角形面积公式解答即可;
(2)作出图形,利用面积相等进行解答.
解答 解:(1)因为 BE⊥AC,
所以 S△ABC=$\frac{1}{2}×AC×BE=\frac{1}{2}×8×3=12$cm2;
(2)如图所示,线段AD就是所求作的高,
因为${S}_{△ABC}=\frac{1}{2}×BC×AD=12$cm2,
所以$\frac{1}{2}×5×AD=12$,
所以AD=$\frac{24}{5}$cm.
点评 此题考查三角形的面积,关键是利用三角形面积相等列出等式进行解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列各式不能用平方差公式法分解因式的是( )
| A. | x2-4 | B. | -x2-y2 | C. | m2n2-1 | D. | a2-4b2 |
10.下列等式不一定成立的是( )
| A. | $\sqrt{\frac{a}{b}}$=$\frac{\sqrt{a}}{\sqrt{b}}$(b≠0) | B. | a3•a-5=$\frac{1}{{a}^{2}}$(a≠0) | C. | a2-4b2=(a+2b)(a-2b) | D. | (-2a3)2=4a6 |
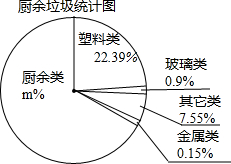 杭州市推行垃圾分类已经多年,但在剩余垃圾中除了厨余类垃圾还混杂着非厨余类垃圾.如图是杭州某一天收到的厨余垃圾的统计图.
杭州市推行垃圾分类已经多年,但在剩余垃圾中除了厨余类垃圾还混杂着非厨余类垃圾.如图是杭州某一天收到的厨余垃圾的统计图.