题目内容
16. 如图,已知在△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9,
如图,已知在△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9,(1)求DC、AB的长;
(2)求证:△ABC是直角三角形.
分析 (1)在Rt△BCD中利用勾股定理求得CD的长,然后在Rt△ADC中求得AD的长,根据AB=AD+DB即可求解;
(2)利用勾股定理的逆定理即可判断.
解答 解:(1)∵在Rt△BCD中,BC=15,BD=9,
∴CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=$\sqrt{1{5}^{2}-{9}^{2}}$=12.
在Rt△ADC中,AC=20,CD=12,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{2{0}^{2}-1{2}^{2}}$=16.
∴AB=AD+DB=16+9=25.
(2)∵AB=25,AC=20,BC=15,
∴AB2=252=625,AC2+BC2=202+152=625,
∴AB2=AC2+BC2,
∴△ABC是直角三角形.
点评 本题考查了勾股定理和勾股定理的逆定理,正确理解定理的内容是关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
6. 把一块直尺与三角板如图放置,若∠1=40°,则∠2的度数为( )
把一块直尺与三角板如图放置,若∠1=40°,则∠2的度数为( )
 把一块直尺与三角板如图放置,若∠1=40°,则∠2的度数为( )
把一块直尺与三角板如图放置,若∠1=40°,则∠2的度数为( )| A. | 130° | B. | 140° | C. | 12° | D. | 125° |
7. 如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
 如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
如图,已知直线a、b被直线c所截,那么∠1的同位角是( )| A. | ∠4 | B. | ∠3 | C. | ∠2 | D. | ∠5 |
11.下列现象不属于平移的是( )
| A. | 乘电梯从2楼到3楼 | B. | 铅球沿直线不滚动运动 | ||
| C. | 铁球从高处自由下落 | D. | 坐滑梯下滑 |
 如图,一副直角三角板顶点重合,若∠ABD=40°,则∠EBC的度数是140°.
如图,一副直角三角板顶点重合,若∠ABD=40°,则∠EBC的度数是140°.
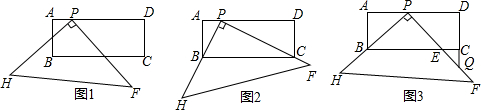
 如图,两个直角三角形重叠在一起,将其中一个三角形沿着BC边平移到△DEF的位置,∠B=90°,AB=10,DH=2,平移距离为3,则阴影部分的面积为( )
如图,两个直角三角形重叠在一起,将其中一个三角形沿着BC边平移到△DEF的位置,∠B=90°,AB=10,DH=2,平移距离为3,则阴影部分的面积为( )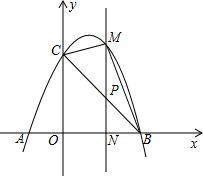 如图,抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,顶点为D,若点P为线段BC上的任意一点(点P不与B、C重合),M为抛物线上一点,且PM∥y轴.
如图,抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,顶点为D,若点P为线段BC上的任意一点(点P不与B、C重合),M为抛物线上一点,且PM∥y轴.