题目内容
6.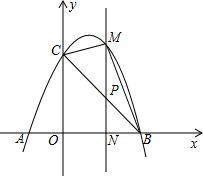 如图,抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,顶点为D,若点P为线段BC上的任意一点(点P不与B、C重合),M为抛物线上一点,且PM∥y轴.
如图,抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,顶点为D,若点P为线段BC上的任意一点(点P不与B、C重合),M为抛物线上一点,且PM∥y轴.(1)求顶点D的坐标;
(2)若点P的坐标为(2,a)时,求△BCM的面积;
(3)若△BCM的面积为最大时,求点P的坐标.
分析 (1)直接利用配方法求出D点坐标即可;
(2)首先求出直线BC的解析式,再利用点P的坐标为(2,a),进而得出P点坐标以及M点坐标,得出MP的长,求出△BCM的面积;
(2)求出△BCM面积的表达式,得出是二次函数,求出其取最大值的条件即可.
解答 解:(1)y=-x2+2x+3=-(x-1)2+4,
故D(1,4);
(2)由抛物线的解析式y=-x2+2x+3,
∴C(0,3),
令y=0,-x2+2x+3=0,解得x=3或x=-1;
∴A(-1,0),B(3,0),
设直线BC的解析式为:y=kx+b,则有:
$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直线BC的解析式为:y=-x+3.
∵点P的坐标为(2,a),
∴a=1,
则P(2,1),
当x=2,则-x2+2x+3=-4+4=3=3,则M(2,3),
故PM=3-1=2,
故S△BCM=S△PMC+S△PMB=$\frac{1}{2}$PM•(xP-xC)+$\frac{1}{2}$PM•(xB-xP)=$\frac{1}{2}$×2×(2+1)=3;
(3)设P(x,-x+3),则M(x,-x2+2x+3),
∴PM=(-x2+2x+3)-(-x+3)=-x2+3x.
∴S△BCM=S△PMC+S△PMB=$\frac{1}{2}$PM•(xP-xC)+$\frac{1}{2}$PM•(xB-xP)=$\frac{1}{2}$PM•(xB-xC)=$\frac{3}{2}$PM.
∴S△BCM=$\frac{3}{2}$(-x2+3x)=-$\frac{3}{2}$(x-$\frac{3}{2}$)2+$\frac{27}{8}$.
∴当x=$\frac{3}{2}$时,△BCM的面积最大.
此时P($\frac{3}{2}$,$\frac{3}{2}$),
点评 此题主要考查了二次函数综合题以及三角形面积求法,解题过程中有若干解题技巧需要认真掌握:第(3)问中求△BCM面积表达式的方法.

 名校课堂系列答案
名校课堂系列答案 如图,已知在△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9,
如图,已知在△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9,