题目内容
6．
把一块直尺与三角板如图放置，若∠1=40°，则∠2的度数为（ ）| A． | 130° | B． | 140° | C． | 12° | D． | 125° |
分析 先根据三角形外角性质计算出∠3=130°，然后根据两直线平行，同位角相等即可得到∠2的度数．
解答 
解：如图，∵∠3=∠1+90°，
而∠1=40°，
∴∠3=130°，
∵a∥b，
∴∠2=∠3=130°．
故选A．
点评 本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．
练习册系列答案
相关题目
16．下列运算正确的是（ ）
| A． | a3•a2=a6 | B． | （-a3）2=a6 | C． | 2a+3a2=5a3 | D． | $3{a^3}÷2a=\frac{3}{2}{a^3}$ |
17．下列四个实数中，绝对值最大的数是（ ）
| A． | -$\sqrt{20}$ | B． | $\sqrt{15}$ | C． | $\root{3}{19}$ | D． | -$\root{3}{62}$ |
如图，直线AB、CD相交于点0，OE平分∠AOD，∠FOC=96°，∠BOF=40°，试求∠AOE的度数．
1．下列命题中，假命题的是（ ）
| A． | a，b，c是直线，若a∥b，b∥c，则a∥c | |
| B． | a，b，c是直线，若a⊥b，b⊥c，则a∥c | |
| C． | a，b，c是直线，若a⊥b，a⊥b，a⊥c，则b⊥c | |
| D． | a，b，c是直线，若a⊥b，b∥c，则a⊥c |
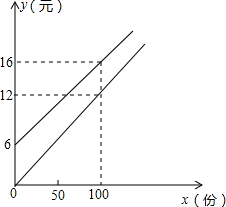我校实行学案教学，需印刷若干份数学学案．印刷厂有甲、乙两种收费方式，除按印数收取印刷费外，甲种方式还需收取制版费而乙种不需要．两种印刷方式的费用y（元）与印刷份数x（份）之间的关系如图所示：
15．若a2-b2=$\frac{1}{4}$，a-b=$\frac{1}{2}$，则a+b的值为（ ）
| A． | -$\frac{1}{2}$ | B． | 1 | C． | $\frac{1}{2}$ | D． | 2 |
如图，已知在△ABC中，CD⊥AB于点D，AC=20，BC=15，DB=9，