题目内容
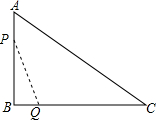 如图在△ABC中,AB与BC垂直,AB=12,BC=24,动点P从点A开始沿AB方向向B点以2/s的速度运动,动点Q从B点开始沿BC向C点以4/s的速度运动,如果P、Q分别同时从A、B出发.
如图在△ABC中,AB与BC垂直,AB=12,BC=24,动点P从点A开始沿AB方向向B点以2/s的速度运动,动点Q从B点开始沿BC向C点以4/s的速度运动,如果P、Q分别同时从A、B出发.(1)如果△PBQ的面积为S,写出S与运动时间t的关系式及t的取值范围.当t为何值时面积S最大,最大是多少?
(2)在P、Q运动过程中当t为何值时△PQB与△ABC相似.
考点:相似三角形的判定与性质
专题:动点型
分析:(1)先用含t的代数式表示出PB、QB再根据三角形的面积公式计算.
(2)令△PQB∽△ACB、△PQB∽△ABC时求t的值即可.
(2)令△PQB∽△ACB、△PQB∽△ABC时求t的值即可.
解答:解:(1)根据题意得BP=12-2t,BQ=4t
∴△PBQ面积为:
S=
(12-2t)4t=4(6t-t2)=-4(t-3)2+36,t取值范围为0<t<6,
当t=3时,S有最大值36.
(2)在P、Q运动过程中,当△PQB∽△ACB时,
=
=
,
2(12-2t)=4t,t=3,
∴t=3,时,△PQB∽△ABC.
同理,当△PQB∽△ABC时,t=
.
综上所述,满足条件的t的值是:3或
.
∴△PBQ面积为:
S=
| 1 |
| 2 |
当t=3时,S有最大值36.
(2)在P、Q运动过程中,当△PQB∽△ACB时,
| PB |
| BQ |
| AB |
| BC |
| 1 |
| 2 |
2(12-2t)=4t,t=3,
∴t=3,时,△PQB∽△ABC.
同理,当△PQB∽△ABC时,t=
| 6 |
| 5 |
综上所述,满足条件的t的值是:3或
| 6 |
| 5 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比值相等的性质.

练习册系列答案
相关题目
若|a|+|b|=0,则a、b的关系是( )
| A、a=b=0 | B、a=-b |
| C、-a=b | D、a=±b |
 如图,在△ABC中,AD平分∠BAC,CE⊥AD,BF⊥AD,求证:
如图,在△ABC中,AD平分∠BAC,CE⊥AD,BF⊥AD,求证: 如图,Rt△ABC中,斜边AB上一点M,MN⊥AB交AC于N,若AM=3cm,AB:AC=5:4,求MN的长.
如图,Rt△ABC中,斜边AB上一点M,MN⊥AB交AC于N,若AM=3cm,AB:AC=5:4,求MN的长.