题目内容
14．
直线l1∥l2，一块含45°角的直角三角板，如图放置，∠1=42°，则∠2等于（ ）| A． | 97° | B． | 93° | C． | 87° | D． | 83° |
分析 根据平行线的性质得出∠2=∠ADE，根据三角形外角性质求出∠ADE，即可得出答案．
解答 解：
∴直线l1∥l2，
∴∠2=∠ADE，
∵∠1=42°，∠A=45°，
∴∠2=∠ADE=∠1+∠A=87°，
故选C．
点评 本题考查了三角形外角性质，平行线的性质的应用，能正确运用定理进行推理是解此题的关键．
练习册系列答案
快捷英语周周练系列答案
相关题目
5．
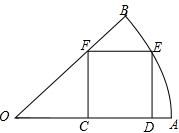如图，在圆心角为45°的扇形内有一正方形CDEF，其中点C、D在半径OA上，点F在半径OB上，点E在$\widehat{AB}$上，则扇形与正方形的面积比是（ ）
如图，在圆心角为45°的扇形内有一正方形CDEF，其中点C、D在半径OA上，点F在半径OB上，点E在$\widehat{AB}$上，则扇形与正方形的面积比是（ ）| A． | π：8 | B． | 5π：8 | C． | $\sqrt{3}$π：4 | D． | $\sqrt{5}$π：4 |
2．下列运算正确的是（ ）
| A． | a2•a2=a4 | B． | （a-b）2=a2-b2 | C． | 2+$\sqrt{2}$=2$\sqrt{2}$ | D． | （-a3）2=-a6 |
如图所示，在一张长为4cm、宽为3cm的矩形纸片上，现要剪下一个腰长2cm的等腰三角形（要求：等腰三角形的一个顶点与矩形的一个顶点重合，另两个顶点在矩形的边上），则剪下的等腰三角形面积为2或$\sqrt{3}$cm2．
6．下列计算正确的是（ ）
| A． | 2（x+y）=2x+y | B． | 2a（a+b）=2a2+b | ||
| C． | 10ab÷（-5a）=-2 | D． | （x-a）（x-b）=x2-（a+b）x+ab |
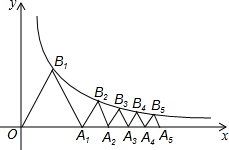如图，点A1、A2、A3、A4、A5、…、A2015在x轴的正半轴上，点B1、B2、B3、B4、B5、…、B2015在双曲线y=$\frac{\sqrt{3}}{x}$上，若△A1B1O、△A2B2A1、△A3B3A2、△A4B4A3、△A5B5A4、…、△A2015B2015A2014均为等边三角形，求△A2015B2015A2014的边长．