题目内容
10.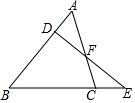 如图,已知△ABC的边AB上有一点D,边BC的延长线上有一点E,且AD=CE.DE交AC于点F,试证明:AB•DF=BC•EF.
如图,已知△ABC的边AB上有一点D,边BC的延长线上有一点E,且AD=CE.DE交AC于点F,试证明:AB•DF=BC•EF.
分析 先作辅助线DG∥BC,然后根据三角形相似的知识可以得到结论成立,从而可以解答本题.
解答 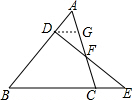 证明:作DG∥BC,
证明:作DG∥BC,
则△ADG∽△ABC,△DGF∽△ECG,
∴$\frac{AD}{AB}=\frac{DG}{BC}$,$\frac{DG}{CE}=\frac{DF}{EF}$,
∵AD=CE,
∴$\frac{AD}{DG}=\frac{AB}{BC}$,$\frac{DG}{AD}=\frac{DF}{EF}$,
∴$\frac{AD}{DG}=\frac{AB}{BC}$,$\frac{AD}{DG}=\frac{EF}{DF}$,
∴$\frac{AB}{BC}=\frac{EF}{DF}$,
∴AB•DF=BC•EF.
点评 本题考查相似三角形的判定与性质,解答本题的关键是明确题意,找出所求结论需要的条件,利用三角形的相似解答.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
20.若关于x的二次函数y=mx2-2x+1的图象与x轴仅有一个公共点,则实数m=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 0或1 |

 已知,如图,CB∥OA,∠C=∠OAB=120°,E、F在CB上,且满足∠FOB=∠FBO,OE平分∠COF,
已知,如图,CB∥OA,∠C=∠OAB=120°,E、F在CB上,且满足∠FOB=∠FBO,OE平分∠COF,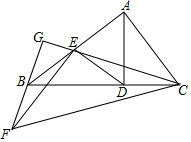 如图,Rt△ABC中,∠BAC=90°,过点A作AD⊥BC于点D,点E为线段AB中点,连接ED,EC将△EDC绕点E旋转,使点D和点B重合,得到△EBF,延长FB、CE相交于点G,若BC=$\sqrt{5}$,则BG=$\frac{\sqrt{5}}{3}$.
如图,Rt△ABC中,∠BAC=90°,过点A作AD⊥BC于点D,点E为线段AB中点,连接ED,EC将△EDC绕点E旋转,使点D和点B重合,得到△EBF,延长FB、CE相交于点G,若BC=$\sqrt{5}$,则BG=$\frac{\sqrt{5}}{3}$.