题目内容
6.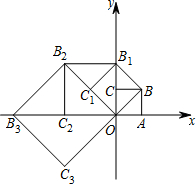 如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则点B6的坐标为(8,-8).
如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则点B6的坐标为(8,-8).
分析 根据勾股定理求出OB的长度,利用正方形的每一条对角线都把它分成两个全等的等腰直角三角形得出B的坐标,再根据题意和图形可看出每经过一次变化,都逆时针旋转45°,边长都乘以$\sqrt{2}$,所以可求出点B6的坐标.
解答 解:∵四边形OABC是一个边长为1的正方形,
∴OB=$\sqrt{2}$,B(1,1),
∵正方形的每一条对角线都把它分成两个全等的等腰直角三角形,
∴OB1=$\sqrt{2}$OB=2=($\sqrt{2}$)2,
∴OB2=$\sqrt{2}$OB1=2$\sqrt{2}$=($\sqrt{2}$)3,B2(-2,2),
根据题意和图形可看出每经过一次变化,都逆时针旋转45°,边长都乘以$\sqrt{2}$,
∴点B6在第四象限的角平分线上,
∵OB6=($\sqrt{2}$)7,
∴点B6的横坐标是$\frac{\sqrt{2}}{2}$×($\sqrt{2}$)7=8,纵坐标是-$\frac{\sqrt{2}}{2}$×($\sqrt{2}$)7=-8,
∴点B6的坐标为(8,-8).
故答案为:(8,-8).
点评 本题主要考查正方形的性质和点的坐标,解答本题的关键是看出每经过一次变化,点Bi都逆时针旋转45°,边长OBi都扩大$\sqrt{2}$倍.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.小明为备战体育中考,每天早晨坚持锻炼,他花20分钟慢跑到离家900米的江边,在江边休息10分钟后,再用15分钟快跑回家,下列图中表示小明离家的距离y(米)与时间x(分)的函数图象是( )
| A. |  | B. |  | C. | 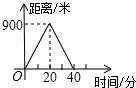 | D. | 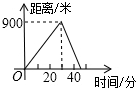 |
8.$\sqrt{\frac{1}{2}+\frac{1}{3}}$的值为( )
| A. | $\frac{1}{6}\sqrt{30}$ | B. | 6$\sqrt{30}$ | C. | $\frac{1}{6}\sqrt{5}$ | D. | 6$\sqrt{5}$ |
 如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是32cm.求:
如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是32cm.求: 如图,点P是正方形ABCD内的一点,连接BP、CP,将△BCP绕点B逆时针旋转至△BAP′,连接AP、PP′,AP′⊥PP′,BP=4,CP=2,求AP的长.
如图,点P是正方形ABCD内的一点,连接BP、CP,将△BCP绕点B逆时针旋转至△BAP′,连接AP、PP′,AP′⊥PP′,BP=4,CP=2,求AP的长.