题目内容
14.不等式组$\left\{\begin{array}{l}{x+3>6}\\{2x-1<10}\end{array}\right.$的正整数解是4和5.分析 先求出不等式组的解集,再求出不等式组的正整数解即可.
解答 解:$\left\{\begin{array}{l}{x+3>6①}\\{2x-1<10②}\end{array}\right.$
∵解不等式①得:x>3,
解不等式②得:x<5.5,
∴不等式组的解集为3<x<5.5,
∴不等式组的正整数解为4和5,
故答案为:4和5.
点评 本题考查了解一元一次不等式组和不等式组的整数解,能求出不等式组的解集是解此题的关键.

练习册系列答案
相关题目
2.多项式x2(x-2)+(2-x)分解因式得结果是( )
| A. | (x-2)(x2+1) | B. | (x-2)(x2-1) | C. | (x-2)(x+1)(x-1) | D. | (x-2)(1+x)(1-x) |
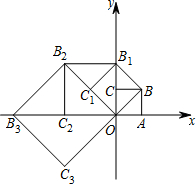 如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则点B6的坐标为(8,-8).
如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则点B6的坐标为(8,-8).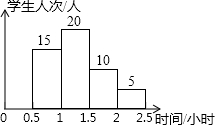 某校为了解学生课业负担的情况,随机抽取了50名七年级学生,调查学生每天完成课外作业所需的平均时间,并绘制了如图所示的频数分布直方图,根据图中信息,完成课外作业所需时间在1.5-2小时的频数是( )
某校为了解学生课业负担的情况,随机抽取了50名七年级学生,调查学生每天完成课外作业所需的平均时间,并绘制了如图所示的频数分布直方图,根据图中信息,完成课外作业所需时间在1.5-2小时的频数是( )