题目内容
16. 如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是32cm.求:
如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是32cm.求:(1)两条对角线的长度;
(2)菱形的面积.
分析 (1)首先证明△ABC是等边三角形,解直角三角形OAB即可解决问题;
(2)菱形的面积等于对角线乘积的一半;
解答 解:(1)菱形ABCD的周长为32cm,
∴菱形的边长为32÷4=8cm
∵∠ABC:∠BAD=1:2,∠ABC+∠BAD=180°(菱形的邻角互补),
∴∠ABC=60°,∠BCD=120°,
∴△ABC是等边三角形,
∴AC=AB=8cm,
∵菱形ABCD对角线AC、BD相交于点O,
∴AO=CO,BO=DO且AC⊥BD,
∴BO=4$\sqrt{3}$cm,
∴BD=8$\sqrt{3}$cm;
(2)菱形的面积=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×8×8$\sqrt{3}$=32$\sqrt{3}$(cm2).
点评 本题考查菱形的性质、等边三角形的判定和性质、解直角三角形等知识,解题的关键是证明△ABC是等边三角形,属于中考常考题型.

练习册系列答案
相关题目
11.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.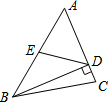 如图,在△ABC中,BD⊥AC于点D,点E为AB的中点,AD=6,DE=5,则线段BD的长为( )
如图,在△ABC中,BD⊥AC于点D,点E为AB的中点,AD=6,DE=5,则线段BD的长为( )
 如图,在△ABC中,BD⊥AC于点D,点E为AB的中点,AD=6,DE=5,则线段BD的长为( )
如图,在△ABC中,BD⊥AC于点D,点E为AB的中点,AD=6,DE=5,则线段BD的长为( )| A. | 5 | B. | 6 | C. | 8 | D. | 10 |

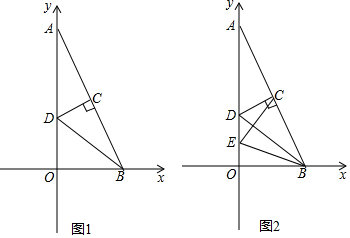
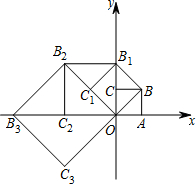 如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则点B6的坐标为(8,-8).
如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则点B6的坐标为(8,-8).