题目内容
8.$\sqrt{\frac{1}{2}+\frac{1}{3}}$的值为( )| A. | $\frac{1}{6}\sqrt{30}$ | B. | 6$\sqrt{30}$ | C. | $\frac{1}{6}\sqrt{5}$ | D. | 6$\sqrt{5}$ |
分析 根据二次根式的性质即可求出答案.
解答 解:原式=$\sqrt{\frac{5}{6}}$=$\frac{\sqrt{30}}{6}$
故选(A)
点评 本题考查二次根式的性质,解题的关键是熟练运用二次根式的性质,本题属于基础题型.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
3.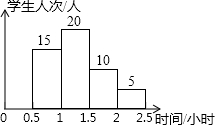 某校为了解学生课业负担的情况,随机抽取了50名七年级学生,调查学生每天完成课外作业所需的平均时间,并绘制了如图所示的频数分布直方图,根据图中信息,完成课外作业所需时间在1.5-2小时的频数是( )
某校为了解学生课业负担的情况,随机抽取了50名七年级学生,调查学生每天完成课外作业所需的平均时间,并绘制了如图所示的频数分布直方图,根据图中信息,完成课外作业所需时间在1.5-2小时的频数是( )
 某校为了解学生课业负担的情况,随机抽取了50名七年级学生,调查学生每天完成课外作业所需的平均时间,并绘制了如图所示的频数分布直方图,根据图中信息,完成课外作业所需时间在1.5-2小时的频数是( )
某校为了解学生课业负担的情况,随机抽取了50名七年级学生,调查学生每天完成课外作业所需的平均时间,并绘制了如图所示的频数分布直方图,根据图中信息,完成课外作业所需时间在1.5-2小时的频数是( )| A. | 15 | B. | 20 | C. | 10 | D. | 2 |
3.把m$\sqrt{-\frac{1}{m}}$化简后的结果为( )
| A. | $\sqrt{m}$ | B. | -m | C. | -$\sqrt{m}$ | D. | -$\sqrt{-m}$ |
20.下列运算正确的是( )
| A. | 6$\sqrt{\frac{a}{2}}$=$\sqrt{3a}$ | B. | -2$\sqrt{3}$=$\sqrt{(-2)^{2}×3}$ | C. | a2$\sqrt{\frac{1}{a}}$=$\sqrt{a}$ | D. | $\sqrt{27}$-$\sqrt{12}$=$\sqrt{3}$ |
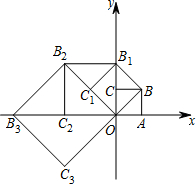 如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则点B6的坐标为(8,-8).
如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则点B6的坐标为(8,-8).