题目内容
17.先化简,再求值:($\frac{{x}^{2}}{x-1}$-x+1)÷$\frac{4{x}^{2}-4x+1}{1-x}$,其中x满足x2-3x=0.分析 先把除法化为乘法,再利用因式分解将原式进行化简,再把x2-3x=0代入求解即可.
解答 解:$(\frac{{x}^{2}}{x-1}-x+1)÷\frac{4{x}^{2}-4x+1}{1-x}$
=$\frac{{x}^{2}-{x}^{2}+1+x-1}{x-1}×\frac{1-x}{(2x-1)^{2}}$
=$-\frac{x}{(2x-1)^{2}}$
∵x满足x2-3x=0,
∴x=0或x=3,
∴把x=0代入原式=0;
把x=3代入原式=$\frac{3}{25}$.
点评 本题考查的是分式的化简求值,解答此题的关键是把x2-3x=0解答,再代入原式求解.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
2.若三角形两边的长分别是8和6,第三边的长是方程x2-2x=10(x-2)的一个实数根,则这个三角形的周长是( )
| A. | 24 | B. | 24或16 | C. | 16 | D. | 22 |
9.下列关于二次函数的说法错误的是( )
| A. | 抛物线y=-2x2+3x+1的对称轴是直线x=$\frac{3}{4}$ | |
| B. | 点A(3,0)不在抛物线y=x2-2x-3的图象上 | |
| C. | 二次函数y=(x+2)2-2的顶点坐标是(-2,-2) | |
| D. | 函数y=2x2+4x-3的图象的最低点在(-1,-5) |
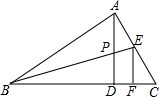 如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,P是AD的中点,BP交AC于点E,EF⊥BC于点F,若AE=3,EC=4,求EF的值.
如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,P是AD的中点,BP交AC于点E,EF⊥BC于点F,若AE=3,EC=4,求EF的值.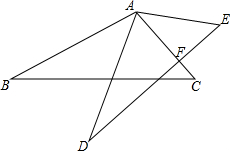 在讲完全等三角形后,数学老师王老师布置了一道数学题:如图所示,已知△ABC≌△ADE,其中∠CAE=40°,∠C=50°,则DE与AC有何位置关系?请说明理由.
在讲完全等三角形后,数学老师王老师布置了一道数学题:如图所示,已知△ABC≌△ADE,其中∠CAE=40°,∠C=50°,则DE与AC有何位置关系?请说明理由.