题目内容
10. 作图与计算:在所给图中仅用直尺和圆规按要求作图(保留作图痕迹,不写作法)
作图与计算:在所给图中仅用直尺和圆规按要求作图(保留作图痕迹,不写作法)(1)作Rt△ABC的外接圆,圆心为O;
(2)以AB为对称轴,作点C的对称点为C′,CC′交AB于E;
(3)当BC=1,AC=2时,计算Rt△ABC绕直线AB旋转一周形成的几何体的侧面积.
分析 (1)作出AB的中点,就是圆心O;
(2)过C作CE⊥AB于点E,然后截取C′E=CE,则C′即为所求;
(3)由AC与BC的长,利用勾股定理求出AB的长,再利用三角形ABC面积的两种求法求出斜边AB边上的高CE的长,将△ABC绕AB所在直线旋转一周,得到一个几何体为两底面重合的圆锥,底面半径都为CE,母线分别为AC与BC,其表面积即为两圆锥的侧面积,利用侧面积公式求出即可.
解答  解:(1)点O就是所求的点;
解:(1)点O就是所求的点;
(2)点C′,E就是所求的点;
(3)在直角△ABC中,AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{1+4}$=$\sqrt{5}$.
∵S△ABC=$\frac{1}{2}$AB•CE=$\frac{1}{2}$AC•BC,
∴CE=$\frac{AC•BC}{AB}$=$\frac{2\sqrt{5}}{5}$,
∴所求几何体的表面积S=π•CE•AC+π•CE•BC=$\frac{6\sqrt{5}}{5}$π.
点评 此题考查了作图-复杂作图,垂径定理,勾股定理,以及圆锥的侧面积公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.下列计算正确的是( )
| A. | $\sqrt{3^2}=9$ | B. | ${(\sqrt{3})^2}=3$ | C. | $\sqrt{(-3)^{2}}$=-3 | D. | ${(\sqrt{3})^2}=9$ |
18.若∠1与∠2互补,∠2与∠3互余,且∠1=140°,则∠3等于( )
| A. | 40° | B. | 130° | C. | 50° | D. | 140° |
 用尺规完成作图(不写作法,保留作图痕迹)
用尺规完成作图(不写作法,保留作图痕迹)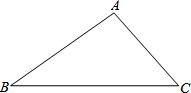 如图,△ABC中,∠B=30°,∠BAC=105°,AB=24,求△ABC的面积.
如图,△ABC中,∠B=30°,∠BAC=105°,AB=24,求△ABC的面积.