题目内容
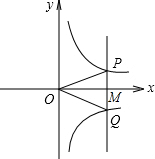 如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数y=
如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数y=| k1 |
| x |
| k2 |
| x |
①∠POQ可能等于90°;②
| PM |
| MQ |
| K1 |
| K2 |
| 1 |
| 2 |
其中一定正确的是( )
| A、①② | B、②③ | C、①③ | D、①④ |
考点:反比例函数综合题
专题:
分析:①点M从点O出发,沿着x轴正方向运动,∠POQ从180°逐渐趋向于0°,因而必存在某一时刻,使得∠POQ等于90°,故①正确;
②易得
<0,
>0,因而
≠
,故②不正确;
③由PQ∥y轴可得OM⊥PQ,k1=OM•PM,k2=-OM•QM,由k1+k2=0可得PM=QM,根据垂直平分线的性质可得OP=OQ,故③正确;
④S△POQ=S△OMP+S△OMQ=
OM•PM+
OM•QM=
(k1-k2)≠
(|k1+k2|),故④不正确.
②易得
| k1 |
| k2 |
| PM |
| QM |
| PM |
| QM |
| k1 |
| k2 |
③由PQ∥y轴可得OM⊥PQ,k1=OM•PM,k2=-OM•QM,由k1+k2=0可得PM=QM,根据垂直平分线的性质可得OP=OQ,故③正确;
④S△POQ=S△OMP+S△OMQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:①点M从点O出发,沿着x轴正方向运动,∠POQ从180°逐渐趋向于0°,
因而必存在某一时刻,使得∠POQ等于90°,
故①正确;
②∵k1>0,k2<0,∴
<0.
∵
>0,∴
≠
,
故②不正确;
③∵PQ∥y轴,
∴OM⊥PQ,|k1|=OM•PM,|k2|=OM•QM
∵k1>0,k2<0
∴k1=OM•PM,k2=-OM•QM.
∵k1+k2=0,
∴OM•PM-OM•QM=0,
∴PM=QM,
∴OP=OQ,
故③正确;
④S△POQ=S△OMP+S△OMQ
=
OM•PM+
OM•QM
=
(k1-k2)≠
(|k1+k2|).
故④不正确.
故选:C.
因而必存在某一时刻,使得∠POQ等于90°,
故①正确;
②∵k1>0,k2<0,∴
| k1 |
| k2 |
∵
| PM |
| QM |
| PM |
| QM |
| k1 |
| k2 |
故②不正确;
③∵PQ∥y轴,
∴OM⊥PQ,|k1|=OM•PM,|k2|=OM•QM
∵k1>0,k2<0
∴k1=OM•PM,k2=-OM•QM.
∵k1+k2=0,
∴OM•PM-OM•QM=0,
∴PM=QM,
∴OP=OQ,
故③正确;
④S△POQ=S△OMP+S△OMQ
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
故④不正确.
故选:C.
点评:此题主要考查了反比例函数的综合应用,根据反比例函数的性质得出|k1|=OM•PM,|k2|=OM•QM是解决③和④的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
把抛物线y=x2-2x-4先向上平移2个单位,再向右平移3个单位,所得的抛物线是( )
| A、y=x2-8x+10 |
| B、y=x2+8x-10 |
| C、y=x2-8x+13 |
| D、y=x2+8x+13 |
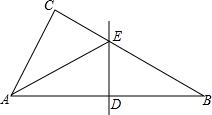 如图,在△ABC中,∠C=90°,E为BC边上一点,将△CAE沿AE折叠,C的对应点D恰好落在AB的中点上,求∠B的度数.
如图,在△ABC中,∠C=90°,E为BC边上一点,将△CAE沿AE折叠,C的对应点D恰好落在AB的中点上,求∠B的度数.