题目内容

已知，在△ABC中，AH是高，内接矩形DEFG的长边在BC上，且BC=48，AH=16，矩形相邻两边之比是5：9，求矩形的面积．
考点：相似三角形的判定与性质,矩形的性质
专题：常规题型
分析：易证△ADG∽△ABC可得
AM
AH
=
EF
BC
，设DE=5x，EF=9x即可解题．
解答：解：设DE=5x，则EF=9x，

AH与DG交于点M，则AM=AH-MH=16-5x，
∵DG∥BC，
∴△ADG∽△ABC，
∴
AM
AH
=
EF
BC
，
16-5x
9x
=
1
3
，
解得x=2，
∴DE=10，EF=18，
∴矩形DEFG的面积为18×10=180．
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质．
练习册系列答案
相关题目
计算：3x4•4x5=
 
；（x+5）2=
 
；（2x+1）（2x-1）=
 
；（a2）3÷a6=
 
．
2014年重庆市共有334000名考生报名参加中考，那么334000这个数用科学记数法表示为
 
．
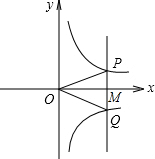如图，若点M是x轴正半轴上任意一点，过点M作PQ∥y轴，分别交函数y=
k1
x
（x＞0）和y=
k2
x
（x＞0）的图象于点P和Q，连接OP和OQ．则下列结论：
①∠POQ可能等于90°；②
PM
MQ
=
K1
K2
； ③当K1+K2=0时，OP=OQ；④△POQ的面积是
1
2
（|k1+k2|）．
其中一定正确的是（　　）
A、①②B、②③C、①③D、①④
如图，△AOB为等腰三角形，顶点A的坐标（2，
5
），底边OB在x轴上．将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B′，点A的对应点A′在x轴上，则点O′的坐标为
 
．
在△ABC中，∠A=30°，∠B=60°，CD⊥AB，D为垂足，AB=8．求CD的值．
小明在研究数字问题时，发现了一个有趣的现象：
已知a，b表示两个正数，把a，b分别作为分子、分母可得到两个分式，如果这两个分式的和比这两个正数的积小2，那么这两个正数的和等于这两个正数的积．
（1）请你用数学表达式补充完整小明发现的这个趣的现象：
已知：a＞0，b＞0，如果
 
，那么
 
．
（2）请你用所学知识证明这个有趣现象．
如图，在正方形ABCD内有一折线段，其中，AE⊥EF，EF⊥FC，并且AE=4，EF=3，FC=5，则该正方形的边长为
 
．
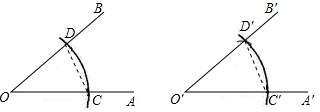请仔细观察用直尺和圆规作一个角等于已知角的示意图，请你根据所学的三角形全等有关的知识，说明画出∠A′O′B′=∠AOB的依据是（　　）
A、SASB、ASA
C、AASD、SSS

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网